【xyz】3つの式の連立方程式の解き方がわかる4ステップ
連立方程式のなかに3つ式があるんだけど??
こんにちは!
中学2年生の連立方程式では、
- x
- y
の2文字がでてきたね!
でも、たまーに、ごくたまーに。
- x
- y
- z
の3文字がでてくる連立方程式もあるんだ。
今日はそんな問題に対応できるよう、
3つの式の連立方程式(xyz)の解き方
を4ステップで解説していくよ。よかったら参考にしてみて。
3つの式の連立方程式の解き方がわかる4ステップ
解き方のポイントは、
「1つの式」をつかって「1つの文字」を消去する
ということさ。
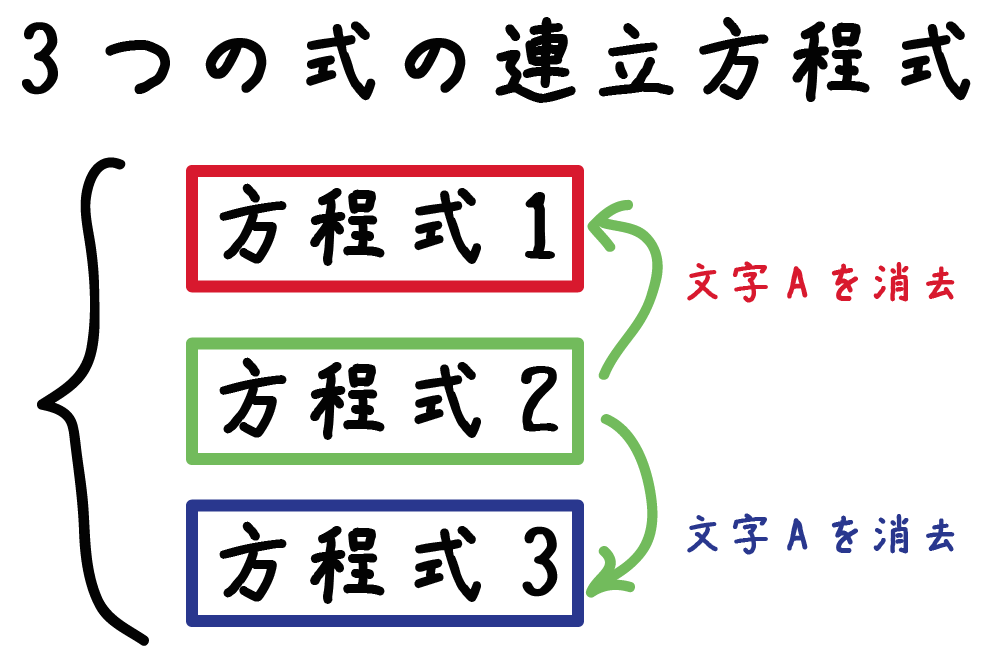
例題をときながらみていこう。
つぎの連立方程式を解きなさい。
x + y – z = -6 ……(1)
2x + 4y + 3z = 9 ……(2)
5x + 3y +z = 4 ……(3)

Step1. 「1つの式」で「文字を1つ」消去する
1つの式だけで文字を1つ消去してみよう。
えっ。どの文字を選んだらいいのかわからないだって??
そういうときは、
なるべく係数が小さい文字をえらんでみて!
加減法で文字が消しやすいからね。
例題でいうと、
すべての係数が1の
x + y -z = -6
を選んでみよう。
そんで、係数が小さい「z」を消してみよう。
(1)式をつかって「z」を消すために、
- (1)式 + (3)式
- (1)式×3 + (2)式
という計算をしてみて。加減法をつかっているよ。
すると、
- 6x +4y =-2
- 5x +7y = -9
の2つの式に進化するよ!
Step2. 文字をさらに1つ消す!
3つの文字が2つになったでしょ??
もうひと頑張りして、
2つの文字を1つにしてみよう!
例題ではStep1で、
- 6x +4y =-2 …….(4)
- 5x +7y = -9 …….(5)
みたいに2つの文字の連立方程式をゲットできたよね。
こいつを加減法で解いてみよう。
「y」を消すために、
(4)式を7倍、(5)式を4倍して両者を引き算してやると、
42x + 28y = -14
-) 20x + 28y = -36
——————–
22x = 22
x =1
になるね!
Step3. 文字を代入しちゃう!
ゲットした解を式に代入してみよう。
代入して方程式をとけばいいんだ。
例題でいうと、(4)式の
6x +4y =-2
に「x =1」を代入してみよう。
すると、
6 × 1 + 4y = -2
となって、
4y = -8
y = -2
になるでしょ。
これでyの解もゲットできたね!
Step4. 文字を2つ代入しちゃう!
文字はあと1つだね。
これまでにゲットした2つの解を「xyz」の連立方程式に代入してやろう。
例題では、
- x = 1
- y = -2
っていう2つの解がわかってるよね??
こいつらをxyzの式に代入してやればいいんだ。
(1)式に代入してみると、
x + y -z = -6
1 -2 -z = -6
z = 5
となったね。
おめでとう!
xyzの解である、
(x, y , z) = (1, -2, 5)
が求まったね。
まとめ:連立方程式から1つずつ文字を消してく!
3つの文字がはいっていたらメンドイ・・・・
そう思っちゃうよね?
ただ、実際に使っているのはこれまで勉強してきた、
なんだ。式が3つに増えて慌てちゃうかもしれないけど、冷静に対処してみよう。
「ちょっと加減法と代入法が心配・・・!」
というときはこれを機に「連立方程式の解き方」を復習してみてね。
そんじゃねー
Ken



