3分でわかる!小数をふくむ連立方程式の解き方
小数がふくまれる連立方程式の解き方わからん!
こんにちは、この記事をかいているKenだよ。回転寿司いいね。
小数の連立方程式ってむずかしいよね??
たとえば次のような問題さ。
例題
つぎの連立方程式を解きなさい。
0.4x + 0.01y = 1
x + y = 22
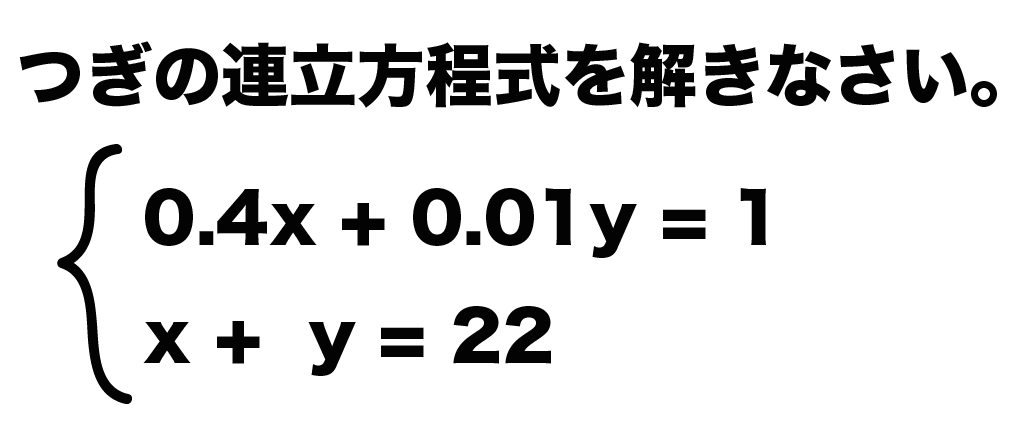
こんな感じで、
どっちかに「小数」がまじっているときは要注意。
こういうときは、連立方程式の解き方でふつうに解く前に、
「あること」
をすればいいんだよ。
今日はそのコツを解説していくねー!よかったら参考にしてみて!
3分でわかる!小数がふくまれる連立方程式の解き方
小数の連立方程式は4ステップでとけちゃうよ。
例題を解いてみよう!
例題
つぎの連立方程式を解きなさい。
0.4x + 0.01y = 1
x + y = 22
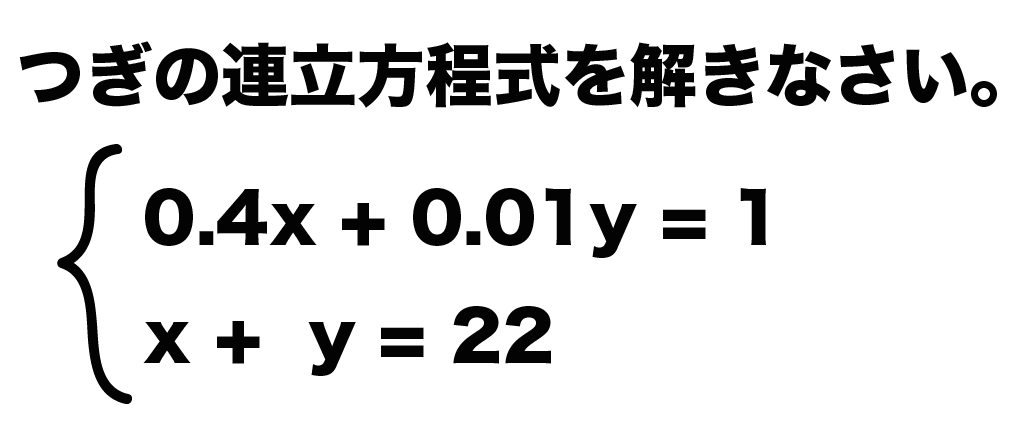
Step1. 小数をけしたる!
連立方程式から小数を消そう!
小数がなかったらフツーの連立方程式と同じだからね。
えっ。どうやって小数を消せばいいのかって?!?
じつは、
いちばん小さな小数の項が消えるように「ある数」を両辺にかける
だけでいいんだ。
かける数は、
いちばん小さい小数が小数点第何位か??
によって違うよ。
つまり、
小数点のうしろに数字が何個あるか
ってことだね。
- 小数点第一位(小数点の後ろに数字1つ):10をかける
- 小数点第二位(小数点の後ろに数字2つ):100をかける
- 小数点第三位(小数点の後ろに数字3つ):1000をかける
のように、かける数をかえていけばいいんだよ。
例題の、
0.4x + 0.01y = 1
をみてみて。
いちばん小さい小数の項は「0.01y」だよね??
これは「.」 の後ろに2つ数字があるから、
小数点第2位の小数だね。
ってことは、100を両辺にかけてやれば小数が消せるのさ。
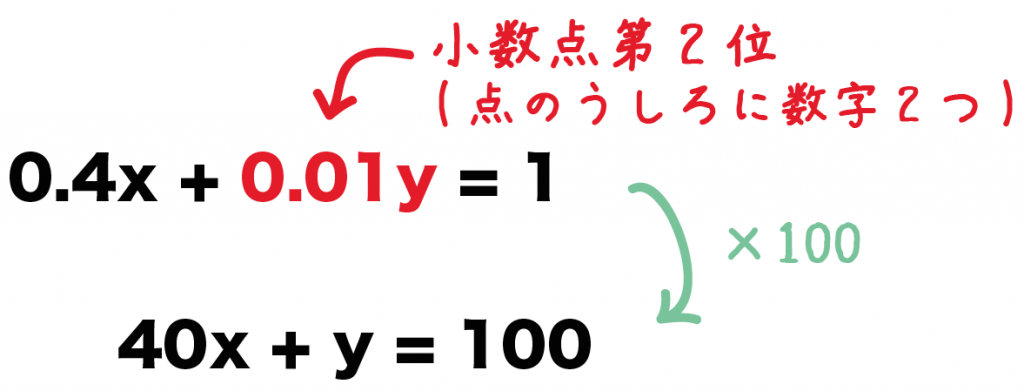
両辺に100をかけてやると、
40x + y = 100
になるね。
これで小数ともおさらば!
Step2. 文字を消す!!
小数の次は「文字」を消しちゃおう。
消し方って2つあったよね??
好きな方で文字を消してみてね。
例題をみてみよう。
小数を消したあとの式は、
40x + y = 100
x + y =22
になる。
yの係数が「1」で同じだから加減法で文字を消そう!
1つ目の方程式から2つ目をひいてやると、
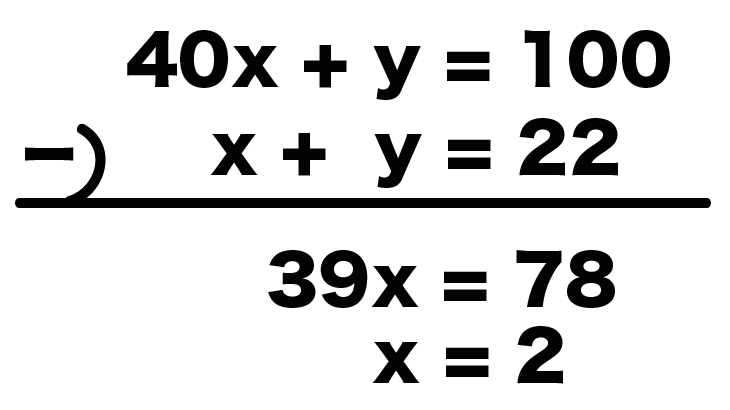
40x + y = 100
– ) x + y =22
——————-
39x = 78
x = 2
になるね!
これでxの解がゲットできた。
あとはyだけだ!
Step3. 解を代入する!
解を式に代入してみよう。
計算が楽なほうを選んでね。
例題では2つ目の式の、
x + y = 22
に解である「x = 2」を代入してみたよ。
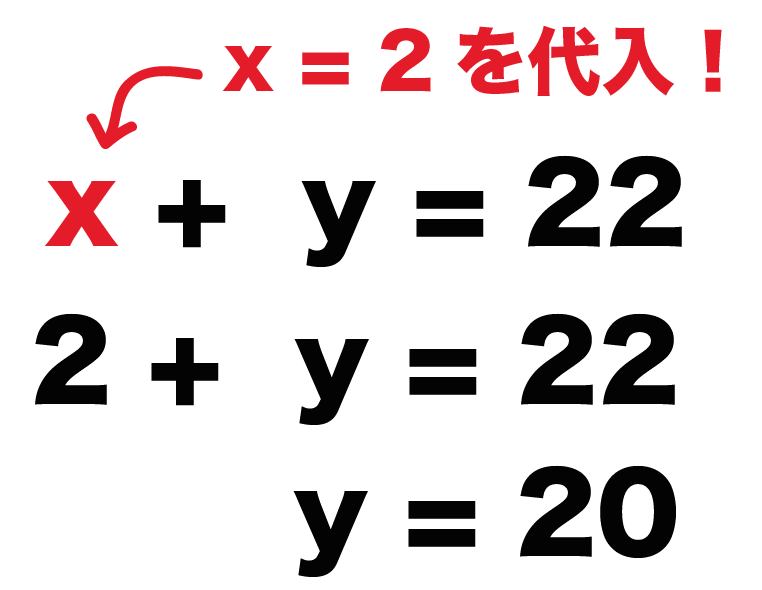
代入して方程式をといてやると、
2 + y = 22
y = 20
になるね!
これでxとyの解のセットである、
(x, y) = (2, 20)
がゲットできたね。
おめでとう!!
まとめ:連立方程式から小数を消すだけでいい!!
小数がはいった連立方程式の解き方はカンタン!
小数を消しちまえばいいんだ。
両辺を10倍、100倍、1000倍とかしてやれば、
とりあえず大丈夫w
小数は消えるからね。
問題を解いてゆっくり慣れていこう!
そんじゃねー
Ken



