等式の変形の解き方がわからない？？
こんにちは！この記事をかいているKenだよ。もやしは安いね。
等式の変形のやり方がわからない・・・・
ってときあるよね？？
うん、わかるよ。その気持ち。
だって、等式の変形なんて見た目がむずかしそうだよね。
しかも、等式の変形なんてなくても生きていけるからね。できれば避けたいはずだ。
今日は、そんな「等式の変形」の問題を3秒ぐらいでとける解き方・やり方を伝授するね。
等式の変形のやり方がわかる3つのステップ
つぎの練習問題をときながら解き方をみていこう。
練習問題
つぎの等式を[ ]内の文字について解きなさい。
12a + 5b = 2 (4a-1) [a]
等式の変形はつぎの3ステップでとけちゃうんだ。
Step1. 分配法則をつかって（）をはずす
等式を分配法則をつかってカンタンにしてみよう。
例題でいうと、右辺の2(4a-1)の（）をはずすことができるよね？？
分配法則で計算してやると、
12a + 5b =2(4a-1)
↓↓
12a + 5b =8a -2
になるよ。
Step2. メイン文字を左辺によせる
等式の変形の問題では「メイン文字」に注目しよう。
メイン文字とは、
〜について解きなさい
という「〜」の部分にあてはまる文字のこと。
つまり、「aについて解きなさい」っていう問題は「a」が「メイン文字」になるってわけ。
このステップでは、
メイン文字を左辺によせる
ってことをしよう。
ぶっちゃけ右でも左でもいいんだけど、左に寄せたほうが解きやすいからね。
メイン文字以外の項は右辺によせてね。
例題でいうと、
aがメイン文字だよね？ だって「aについて解きなさい」って言ってるからね。
aがついている項を左辺によせればいい
ってことさ。
12a + 5b = 8a -2
という等式で、aがついている項を左辺に、それ以外の項を右によせてみよう。
すると、
12a – 8a = -2 -5b
になるね！
そんで、この等式の両辺の同類項をまとめてやると、
4a = -2 – 5b
になるね！
Step3. メイン文字の係数で両辺を割る！
メイン文字の係数で両辺をわってあげよう。
つまり、
メイン文字をちょっとスリムにしてやるってことさ。
コイツはちょっと太りすぎてるからね。
係数でわってメイン文字だけを残してあげよう。
例題のメイン文字の係数は「4」だよね？？
こいつで両辺をわってあげよう。
4a = -2 – 5b
の両辺を「4」でわってやると、
a = (-2 -5b)/4
になるね！
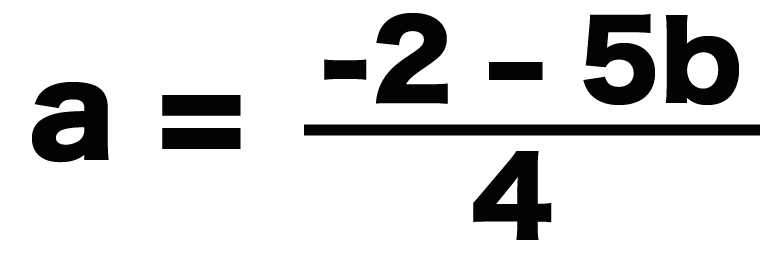
むちゃくちゃ左辺がすっきりしたっしょ？？ だって、メイン文字しか残ってないからね。
これでこの例題の等式は、
aについて解けた！
ってことになるよ。
おめでとう！！これで等式の変形も完ぺきだね。
まとめ：等式の変形ではメイン文字を左辺に！
等式の変形は意外とシンプル。
〜について解きなさい、
の「〜」の文字を左辺によせて両辺を係数でわるだけ！
中1数学で勉強した「移項」さえマスターしておけば大丈夫さ。
等式の変形はテストに出やすいから、解き方をよーく復習しておいてね。
そんじゃねー
Ken
