イリエダ

こんにちは、イルカの妖精イリエダよ。

前回は10進数から2進数への変換だったわね。

tomo

【高校情報】10進数から2進数への変換方法〜なぜ2で割る？余りは何者？〜

🕒️2026年2月17日

 こんにちは、イルカの妖精イリエダよ。みんな、10進数 から2進数 の変換、不安になってない？大丈夫、今日は簡単な方法を一緒に勉強していくわよ。 簡単にできる！10進数から2進数への変換方法今回は例として、10進数の「13」を変換する場合を考えるわ。 ステップ1:  「2」で割り続けるまずは、10進数の数を2で割り続けましょう。「余り」を記録することを忘れないでね。  例えば、10進数の「13」を変換する場合なら、 13 ÷ 2 = 6 余り 1 6 ÷ 2 = 3 余り 0 3 ÷ 2 = 1 余り 1 1 ÷ 2 = 0 余り 1こんな感じ...

今日は逆！

2進数から10進数に戻してみるわよ。

実はこっちのほうがシンプルかもしれないわ。

簡単にできる！2進数から10進数への変換方法

今回は例として、2進数の「10101」を10進数に戻してみましょう。

ステップ1: 右から順番に「2のかたまり」を確認する

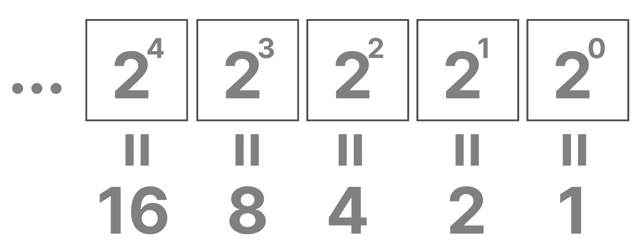
2進数は、右から順番にこういう意味を持っているの。

• 2⁰ = 1
• 2¹ = 2
• 2² = 4
• 2³ = 8
• 2⁴ = 16

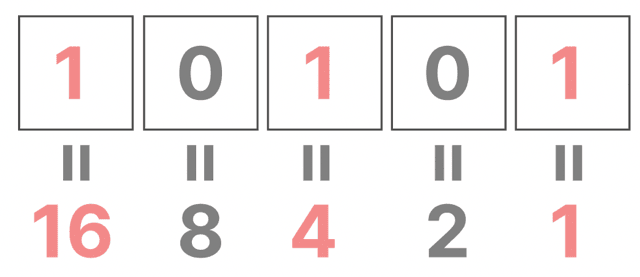
「10101」を右から見ると、

• 1 × 16
• 0 × 8
• 1 × 4
• 0 × 2
• 1 × 1

という意味になるのよ。

ステップ2: 1が立っているところだけ足す

16 + 4 + 1 = 21

だから、

10101₂ = 21₁₀

になるの。

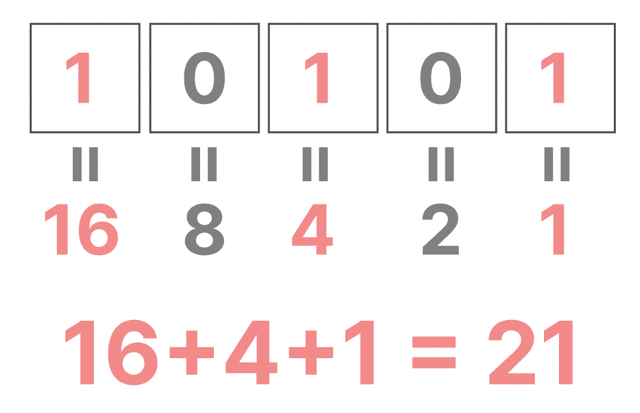
なぜ足すだけで2進数から10進数への変換できるの？

オッケー、案外2進数から10進数への変換も簡単ね。

でも、なぜこのやり方で2進数から10進数へ変換できるのか興味があるでしょ？？

これからバンバンお世話になってくわけだから、その仕組みを知っておくに越したことはないわ。

さて。

10進数の「21」を思い出してみましょう。

21は、

• 2 × 10
• 1 × 1

つまり、

21 = 2×10¹ + 1×10⁰

だったわね。

この仕組みは2進数も同じよ。

10101 = 1×2⁴ + 0×2³ + 1×2² + 0×2¹ + 1×2⁰

という意味ね。

それぞれの桁が「2のかたまりを何個使うか」を表しているの。

だから、そのかたまりを全部足せば10進数に戻るというわけ。

10進数だろうが2進数だろうが100進数だろうが、

各桁が「その基数のかたまりを何個使っているか」を表している

ということに違いはないのね。

10進数なら10のかたまり。

2進数なら2のかたまり。

違うのは「基準の数」だけなのよ。

イリエダ

どう？2進数で迷ったら、普段使い慣れている10進数に戻ってみて。さすれば、進数は怖くないはずよ

そんじゃあね！