【中学数学】箱ひげ図の書き方をわかりやすく解説
「箱ひげ図の書き方」を教えてほしい!!

中学数学の「データの活用」で出てくる箱ひげ図。
名前のインパクト、強すぎますよね。
箱に、ひげ、っすからね。
たぶん、こんなキャラクターイメージしちゃったんじゃないっすか。

でも、いえ。
箱ひげ図はキャラ名ではありません。
数学用語の一種なんです。
えっ、名前からしてゼッタイ難しそうですって??
安心してください。
箱ひげ図は、
四分位数がわかっていれば描けます。
今日は、
「箱ひげ図の書き方(中学数学)」
を、ステップを踏んでわかりやすく解説します。
~もくじ~
- 箱ひげ図ってなに??
- 箱ひげ図を書くために必要なもの
- 箱ひげ図の書き方
- よくあるミスと注意点
中学数学に出てくる「箱ひげ図」ってなに??
まず基本から。
箱ひげ図とは、
データの散らばり方を、ひと目で表す図
です。
サンプルを出すとこんな感じっすね。
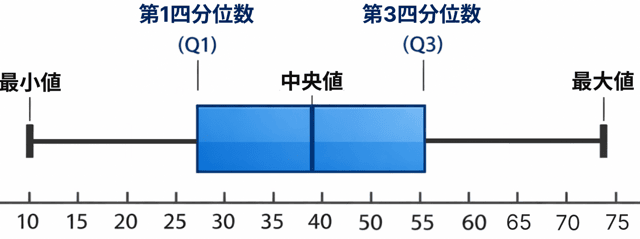
どう?? 全然ヒゲっぽくないでしょ。
この箱ひげ図は、
- 小さい値
- 大きい値
- 中央値
- データの広がり
が一気にわかるのが特徴。
だからテストでもよく出るんすね。
箱ひげ図を書くために必要な5つの数
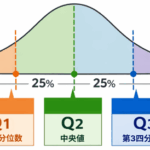
箱ひげ図を書くために必要なのは、次の5つの数です。
- 最小値
- 第1四分位数(Q1)
- 中央値(Q2)
- 第3四分位数(Q3)
- 最大値
この5つがそろえば、箱ひげ図は完成します。
えっ。ちょっと無理??
そんなときは中央値の求め方、
四分位数の求め方を復習しておきましょう。
箱ひげ図の書き方【基本手順】
では、実際に書いていきましょう。
まず、次のようなデータがあるとします。
9, 3, 11, 6, 5, 8, 13
箱ひげ図の書き方は次の6ステップ。
1. データを小さい順に並べる
オッケー、まずは小さい順に並び替え。
すると、
3, 5, 6, 8, 9, 11, 13
こうなりますね。
2. 四分位数を求める
次は、四分位数を求めます。
すると、こんな感じ。
- 最小値:3
- 第1四分位数 Q1:5
- 中央値 Q2:8
- 第3四分位数 Q3:11
- 最大値:13

やり方は四分位数の求め方を読んでみてね。
3. 数直線を書く
値の範囲が入るように、横に数直線を書きます。
ルールは簡単。
最小値〜最大値を必ず含むようにすればいいんす。
- 今回は、
- 最小値:3
- 最大値:13
なので、数直線は「3 〜 13」をカバーする範囲にします。
メモリの間隔は・・・そうだな、2にしておこうか。辛いし。
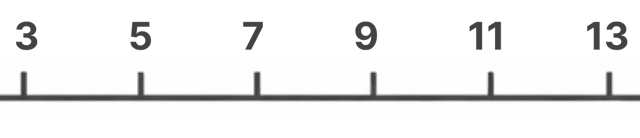
右端の矢印ヘッドは書かなくて大丈夫。
4. 箱を書く
オッケー、次はいよいよ箱です。
まず、Q1 から Q3 までを「箱」で囲みます。
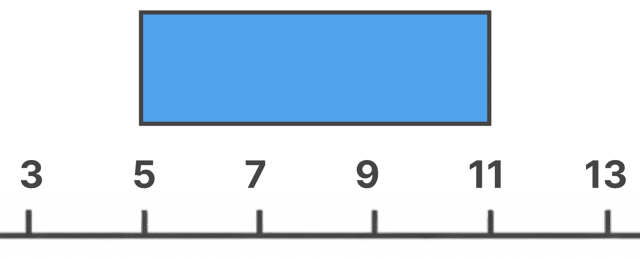
今回は
- 第1四分位数 Q1:5
- 第3四分位数 Q3:11
でしたよね。だから、こんな感じのボックスが登場。
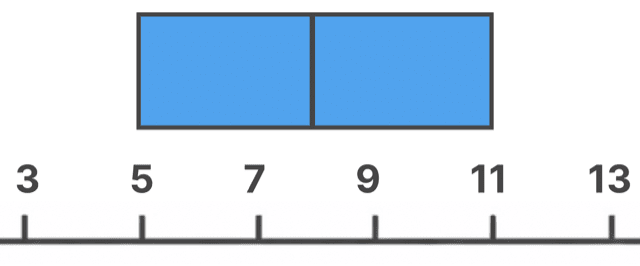
5. 中央値の線を書く
そして、箱の中に中央値の線を引こう。
今回は
- 中央値 Q2:8
だから、こんな感じ。
6. ひげを書く
さて、お待ちかねのひげ、きました。
箱ひげ図の「ひげ」って、これっすね。
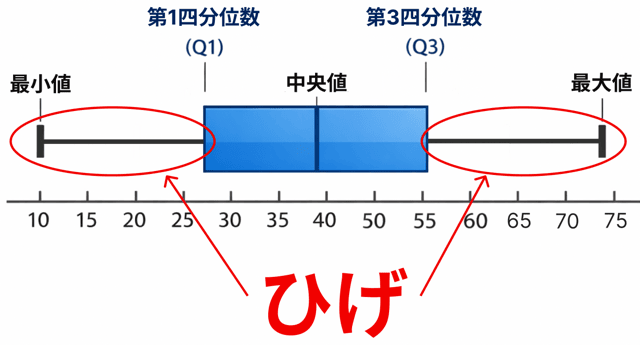
ひげの書き方は
箱の左端(Q1)から最小値まで線を引く。
箱の右端(Q3)から最大値まで線を引く。
です。
今回の場合は、
- 最小値:3
- 最大値:13
でしたから、こんな感じ。
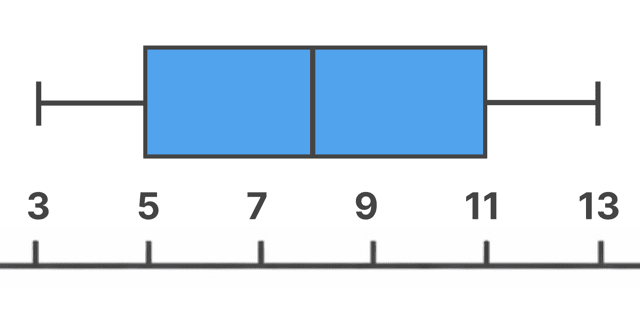
うん、はい。
これで、
箱ひげ図の完成!

箱ひげ図でよくあるミス・注意点
テストで多いミスをまとめます。
- 数直線の目盛りが不正確
- 箱の位置がずれている
- 中央値の線を書き忘れる
- 最小値・最大値をひげにしない
特に、
箱は Q1 ~ Q3、ひげは端まで。
ここを間違えないようにしましょう。
箱ひげ図で何が読み取れるの??
箱ひげ図を見ると、
- 中央値の位置
- データの散らばり
- 四分位範囲の大きさ
がすぐにわかります。
箱が長い → ばらつきが大きい
箱が短い → データが集中
という見方も、テストでよく聞かれますので要記憶。
まとめ:箱ひげ図の書き方、これで完璧!
箱ひげ図は、
- 四分位数を求めて
- 箱を書いて
- ひげを伸ばす
だけでした。
見た目は難しそうですが、中身はシンプル。

そんじゃねー