【中学数学】四分位数の求め方を奇数・偶数でわかりやすく図解解説
「四分位数の求め方」を教えてほしい!!

中学数学で登場する「四分位数(しぶんいすう)」。
中央値はなんとなくわかるけど、
四分位数??
なんか急に専門用語っぽい〜
なんて思っちゃいますよね。
しかも問題をよく見ると、
- データの個数が奇数
- データの個数が偶数
で、やり方が変わるみたいで混乱しがちです。
今日は、
「四分位数の求め方(奇数・偶数それぞれ対応)」
を中学生向けにやさしく解説します。
~もくじ~
- 四分位数ってなに??
- 四分位数を求める手順
- データが奇数のとき
- データが偶数のとき
- よくある注意点
中学数学にでてくる「四分位数」ってなに??
そもそもからいきましょう。
四分位数とはずばり、
データを4つに分けたときの区切りになる数
です。
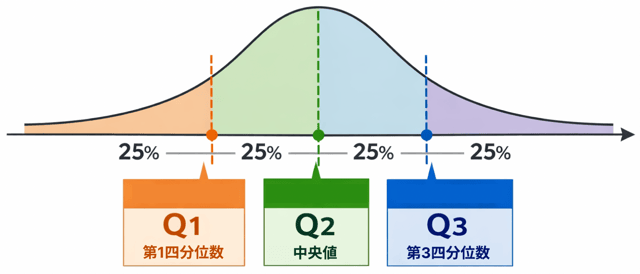
ポイントはここ ↓
小さい順に並べたデータを4等分する
ってこと。
そのときに出てくるのが、
- 第1四分位数(Q1)
- 第2四分位数(Q2)=中央値
- 第3四分位数(Q3)
です。
中学数学では、Q1 と Q3 を求められることが多いです。
四分位数の求め方【奇数・偶数対応】
四分位数は、次の3ステップで求めます。
- データを小さい順に並べる
- 中央値(Q2)を求める
- 左右それぞれの中央値を求める
ここから、奇数か偶数かで少しだけ分かれますよ。
データの個数が「奇数」のとき
たとえば、次のデータの四分位数を求めてみましょう。
9, 3, 11, 6, 5, 8
まず、小さい順に並べます。
すると、
3, 5, 6, 8, 9, 11
になる。
そして、データの真ん中は「8」。
これが中央値(Q2)ってわけっすね。
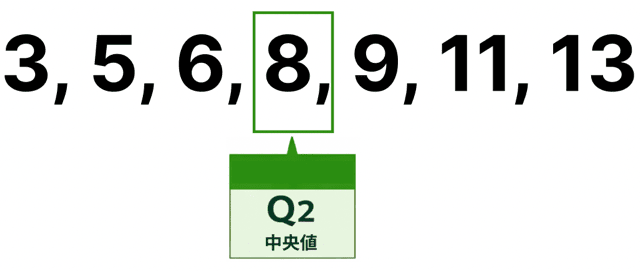
そして、中央値を除いて左右に分けます。
- 左:3, 5, 6
- 右:9, 11, 13
それぞれの中央値は、
- 第1四分位数 Q1 = 5
- 第3四分位数 Q3 = 11

これで四分位数が求まりましたね。
データの個数が「偶数」のとき
次は偶数の場合です。
6, 13, 5, 9, 3, 8, 11
さて、もう一度小さい順に並べます。
3, 5, 6, 8, 9, 11, 13
この場合だと、真ん中2つは「6」と「8」。
この2つの平均が中央値(Q2)になるんすね!
つまり、
(6 + 8) ÷ 2 = 7
です。

だがしかし、
中央値の値は、分けるための目安
として使うってポイントに注意です。
「左右それぞれの中央値を求める」っていう最後のステップでは、中央値は一旦脇に置来ましょう。
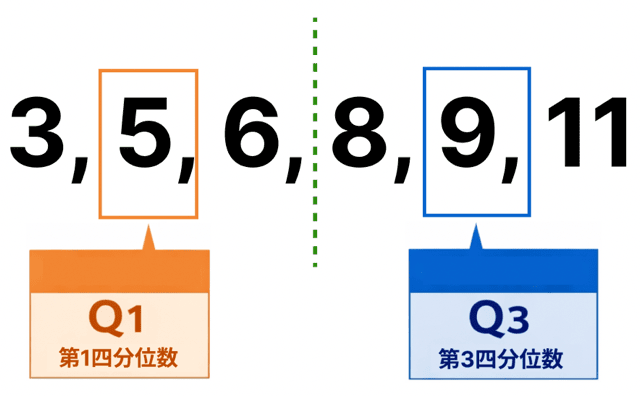
ってことで、中央値を無視して左右にわけると、
- 左:3, 5, 6
- 右:8, 9, 11
それぞれの中央値は、
- 第1四分位数 Q1 = 5
- 第3四分位数 Q3 = 9
となります。
まとめ
テストで間違えやすいポイントをまとめます。
- 必ず小さい順に並べる
- 奇数のときは中央値を除く
- 偶数のときは中央値を数として使わない
- 四分位数は中央値の応用
この4つを意識すればOKです。
四分位数は、
- 中央値をベースに
- 左右の中央値を見る
だけでした。
このあと、
- 四分位範囲
- 箱ひげ図
へとつながっていきます。

そんじゃねー



