【中学数学】三角錐の高さの求め方がわかる4つのステップ
三角錐の高さの求め方がわからない!
こんにちは、この記事をかいているKenだよ。ペプシはダイエット一択だね。
三角錐の高さを求めなさい!
っていう問題はたまに出てくるね。たとえば次のように出題されることがあるよ。
例題
つぎの三角錐ABCDがある。底面を三角形ACDとしたときの高さを求めて!
- AB = 6 cm
- BC = 6 cm
- BD = 6 cm
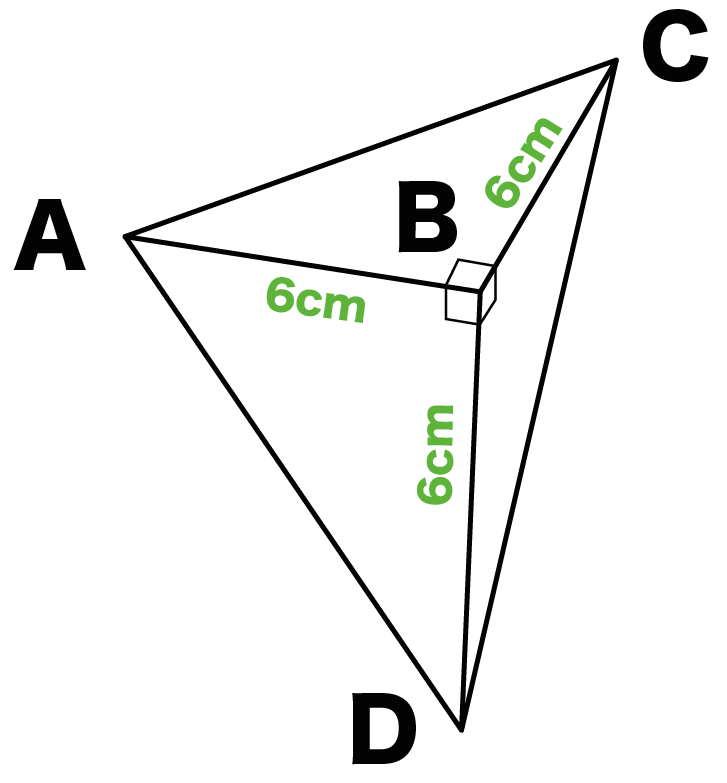
つまり、
頂点Bから三角形ACDにおろした垂線の長さを求めろ!
ってことだね。
三角錐の高さの求め方がわかる4つのステップ
「三角錐の高さ」はつぎの4ステップで計算できるよ。
Step1. 三角錐の体積を計算する!
まずは三角錐の体積を求めてみよう。
どの「底面積」と「高さ」を使っても大丈夫。
例題でいうと、
- 三角形ABCを底面
- BDを高さ
とすれば三角錐ABCDの体積を求めることができるね。
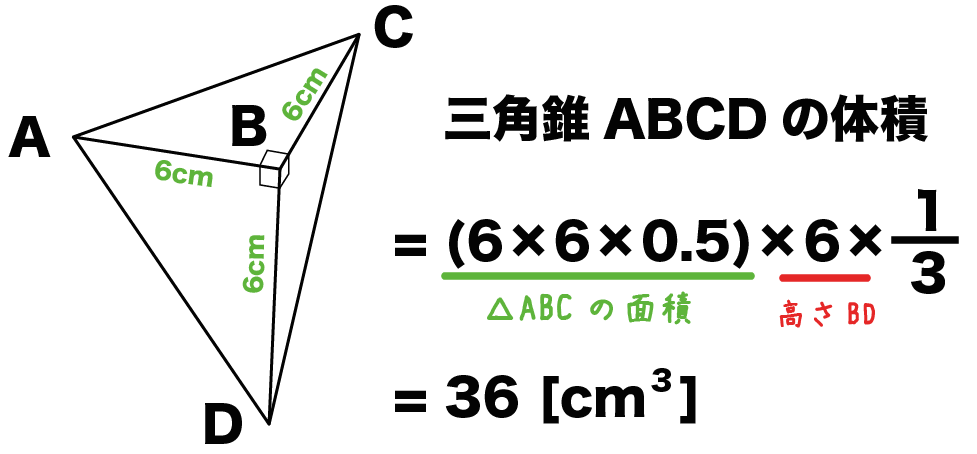
求め方は「底面積×高さ×1/3」だから、
(6×6×0.5)×6×1/3
= 36 [cm^3]
になるね!
Step2. 底面積を求める!
問題で指定されている「底面積」を求めよう!
例題では、
「三角形ACD」を底面とするときの高さ
っていう指定されているよね??
だから、三角形ACDの面積を計算してやればいいんだ!
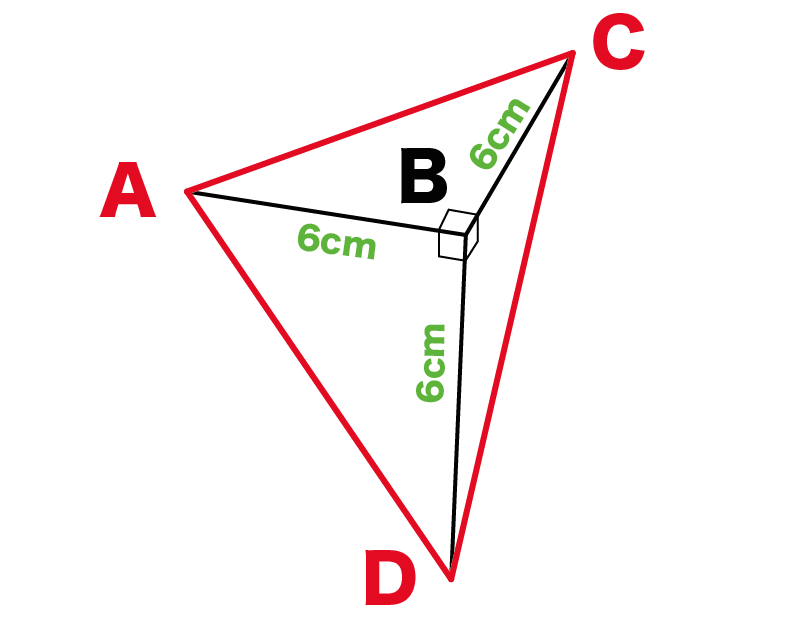
AC、AD、CDの長さを三平方の定理をつかって計算してみると、
ぜんぶ「6√2」になるよね。
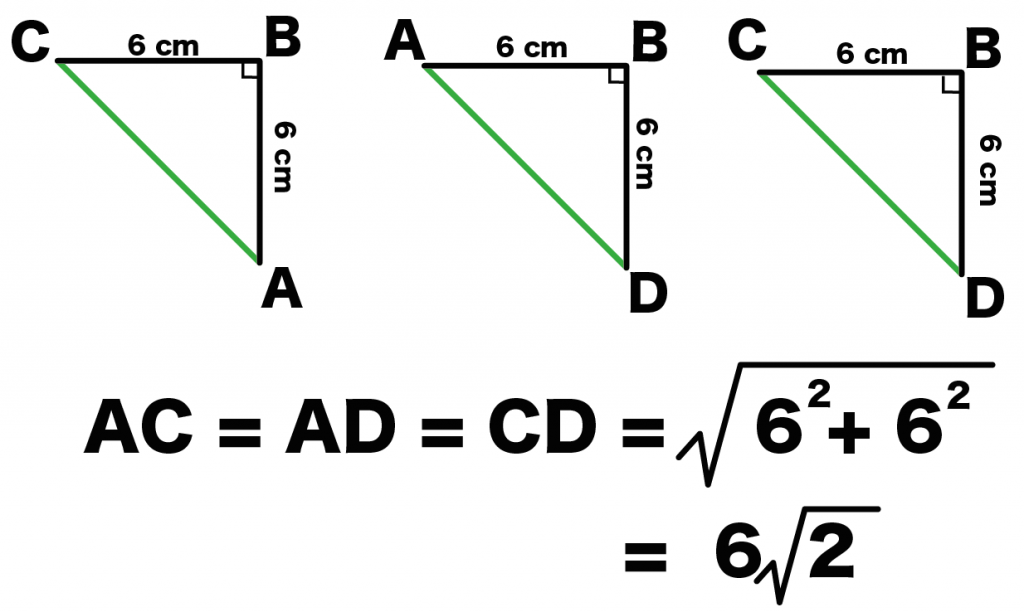
ってことは、三角形ACDは1辺が6√2の正三角形ってことだ!
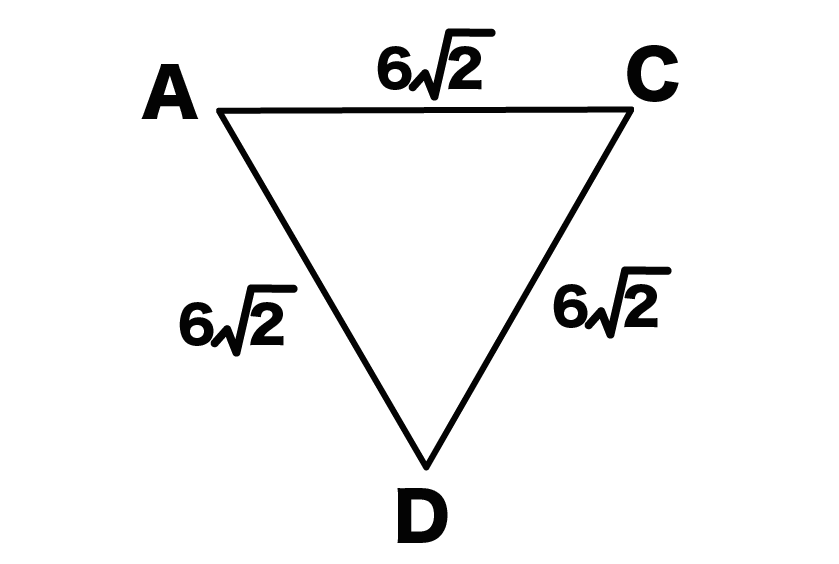
こいつの面積を求めてあげよう。
三平方の定理をつかって高さを求めて(3√6)、面積を計算すると、
6√2×3√6×0.5
= 18√3 [cm^2]
になるね!
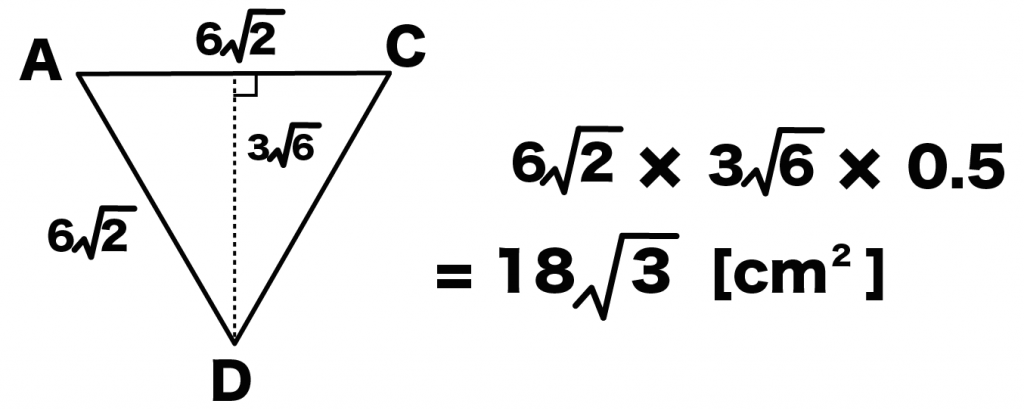
Step3. 方程式をたてるっ!
三角錐の高さ(指定された底面からの)についての方程式をつくってみよう。
つまり、
「三角錐の高さ」を変数と置いた方程式ってことだね。
そいつを解けば、三角錐の高さが求められるってことになる。
例題をみてみよう。
頂点Bから三角形ACDに垂線をおろしたとき、三角形ACDと垂線の交点をHとする。
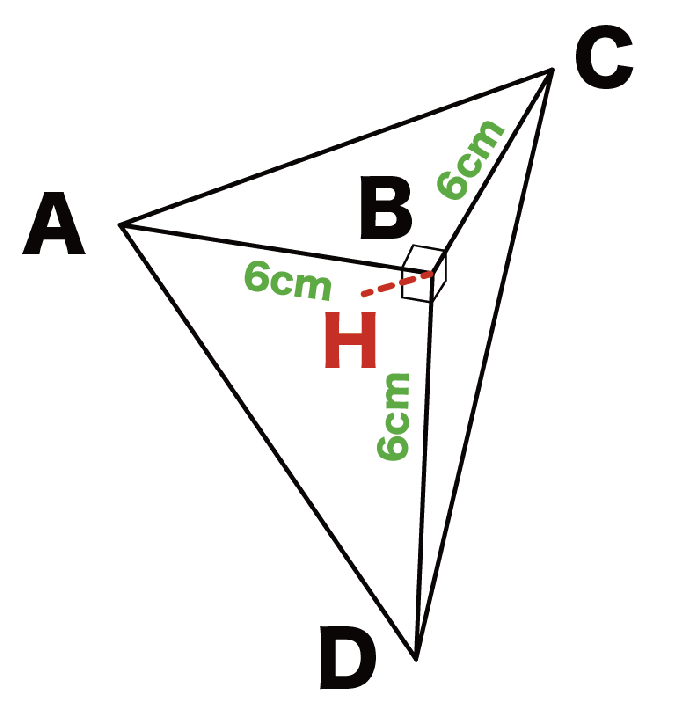
このとき、三角錐ABCDの高さはBHになるよね。
BHの長さを変数とおいて方程式とたててやると、
(△ACDを底面とした時の体積)=(△ABCを底面とした時の体積)
1/3 ×18√3 × BH = 36
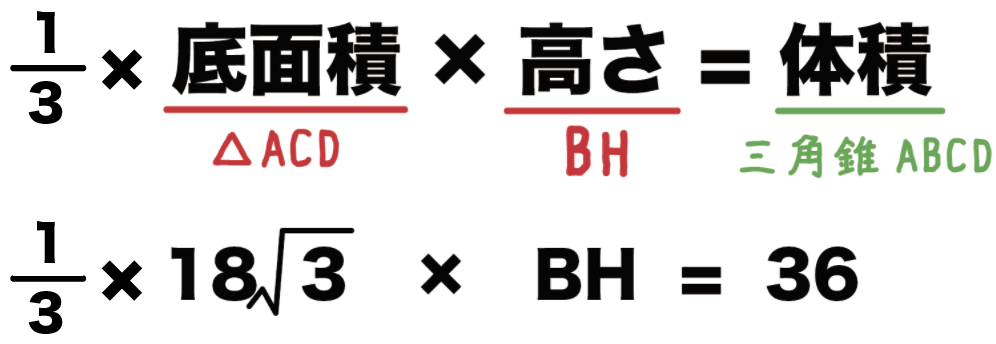
ってなるよ。
Step4. 方程式を根性でとく
あとはStep3でたてた方程式をといてあげるだけ!
方程式の解き方の基本を思い出しながら慎重にといてみてくれ。

1/2 × 18√3 × BH = 36
っていう方程式を解くと、
BH = 2√3
っていう解がゲットできるね。
これが「底面を△ACDとしたときの三角錐の高さ」だね!
おめでとう。
まとめ:三角錐の高さは方程式をたてて算出するっ!
三角錐の高さの求め方はどうだった??
「体積」と「底面積」を計算して方程式をつくるだけさ。
慣れれば5分以内に高さをゲットできるようになるはずだ。
テスト前によーく復習しておこう!
そんじゃねー
Ken


