中学3年生が勉強する数学単元8つのまとめ
中学3年生で学習する数学の単元はどれだ!?
中学生活もあと一年。中学3年生になると進路のことだとか、恋のことだとか、体育祭のことだとか気になりだす頃です。中学生活の中でもっとも忙しく、もっとも思い出に残る一年なんかじゃないですかね!

・・・・・・ところが、ですよ。ところが!
数学、という魔の学問だって忘れちゃいけません。とくに中学三年生なってから勉強する数学は1年生、2年生のころと比べてかなりパワーアップしています。
し、しかも迫りくる高校受験ではかなりの頻度で出題されます。こんな状況で、もし、もしですよ?? 中学3年生のときに数学の学習に手を抜いていたらどうなってしまうでしょう!? 想像するだけできつそうですね。
そこで、今日は、
中学校3年生のときに勉強する数学の単元8つをきれいに華麗にまとめてみました。
これから中学3年生になる中学生の方や、テスト前に中学三年生で勉強した数学の単元を復習したい方。そんな方々の参考になれば嬉しいです。教科書に掲載されている中3数学の単元は以下の8つです。
- 式の展開と因数分解
- 平方根
- 二次方程式
- 二次関数
- 図形と相似
- 円の性質
- 三平方の定理
- 標本調査
8つも数学の単元があって正直目がくらみそうです。ただ、がんばって諦めずに8つの単元を数学のジャンル別に分類してみました。す、すると、
- 数学の基礎
- 代数学
- 幾何学
- 統計学
の4つの数学ジャンルにわけることができたのです。今回は中学3年生の数学単元をわかりやすく4つの種類ごとに紹介していきます。
それでは上から順番に見ていきましょう!
中3数学単元で勉強する「数学基礎」
1つ目に勉強する単元は「数学の基礎」です。中3の数学単元で学習する内容の一つに「数学の基礎を勉強するための基礎」なる単元が登場します。
それは、
平方根(square root)
です。平方根とは簡単にいってしまえば、
二乗すると「ある数」になる数
です。なんだかむちゃくちゃ分かりづらいですね。 たとえば、√2 でしたら、√2を二乗してやると「2」になるわけです。つまり、二乗すると√記号の中身の数字に変化する、というわけですね!
えっ。なぜ平方根という基礎を中学三年生で学習するのかですって!?
それはのちのち勉強する「二次方程式」という単元で必要になるからです。平方根の知識がないと二次方程式をどう汗をかいても解くことはできないのです。
まずはこの数学の基本となる概念を押さえておきましょう。
中3数学で登場する「代数学」は3つの単元
2つ目に勉強していくのが「代数学(algebra)」というジャンル。中2数学単元の記事などで説明しましたが、
数字を文字でおきかえて考え事をする
という数学の学問です。 リアルの数字を文字(aとかb)で置き換えることによって、求めたい値を抽出したり、身近なことがらを一般化したりできます。
たとえば、ぼくの財布の中身を代数学を用いて表現してみましょう。ひと月の稼ぎは7万円しかないです。デートに行く回数をひと月あたりx回とします。一度のデートには6000円かかるので、
70000 – 6000x
という文字式がぼくの財布の中身を表しています。 つまり、財布の中身を文字で一般化してやることで、デートの回数に応じた財布の中の残金がわかるというわけですね。ふむふむ、すこし興味深い。
中学三年生で登場する「代数学」の単元は以下の3つです。
式の展開と因数分解
中学三年生の数学でまず初めに勉強するのがこの単元。ここで勉強する内容は以下の2つです。
- 「かけ算」だらけの文字式を「たし算」へ
- 「たし算」だらけの文字式を「かけ算」へ
ほら? とてもシンプルですよね。αの行為を数学では「展開 (expand)」といい、βの行為を「因数分解(factorization)」と呼んでいます。この2つが中学3年生で学習する数学の基礎の部分です。ここを理解しておかないと中盤に登場する「二次方程式」でつまづくことになってしまいますよ!
二次方程式
おつぎに登場するのが「二次方程式(quadratic equition)」という数学の単元です。これは文字通り、
次数が2である方程式
のことです。中学1年、2年で勉強してきた数学では「次数が1次」の場合のみでした。二次方程式とはたとえば、
式
のような感じです。かなりごっつくて腕力がありそうな数式ですね。
だがしかし、です。
これまでに勉強した「平方根」と「因数分解」をしっかりマスターしていればなんのこっちゃありません。方法さえ覚えてしまえばカップラーメンより簡単です。あ、おいしいかは不明ですけど。
ただ、以上の2つの単元をまだ完全に修得していない方にとってはかなりキツいかもしれません!勇気を持って復習してみましょう。
二次関数
3つ目に代数学の分野で勉強するのは「二次関数(quadratic function)」です。これも二次方程式のときと同様、非常にシンプル。つまり、
次数が2次の関数の勉強
というわけです。中学3年生になるまで比例、一次関数と学んできました。中学数学の集大成の三年生では、次数を二次まで増やした、
式
のような関数に挑戦するというわけですね。むずかしいように聞こえますが、勉強する内容はこれまでと一緒です。
- 関数のグラフをかく
- 関数の正体をあばく
です。この2つができれば中学で学習する関数なんてイチコロです!
中学校3年生で勉強する「幾何学」は3つの単元
幾何学(geometry)とは超シンプルにいってしまえば、
図形のお勉強
です。三角形とか四角形をこれでもか!というほどいじくりまわす数学のジャンルです。中学3年生のときに勉強する幾何学は以下の3つの単元となっています。
図形と相似
「掃除(そうじ)」ではなく「相似(そうじ)」をここでは勉強します・・・・
中学の数学の先生がこんなギャグですべっていたのを今でも思い出せます。
そう、ここで勉強するのは幾何学の一つのジャンルである「相似(similarity)」です。相似とはいわば拡大と縮小の関係のこと。たとえば、下の正方形くんと、
その子供の正方形ちゃんは、
相似の関係にある、と言うことができます。なぜなら、両者は拡大・縮小の関係にあるからです。大きくすれば一緒。小さくすれば一致する。そんな図形同士の複雑な関係について勉強していきます。
2つの相似な図形はどの程度の比率になっているのか?? また、どんな条件をみたす図形同士が「相似」ということができるのか!?
そんなことに注目しながら勉強をすすめてみてくださいね。
円の性質
おつぎは「円(circle)」についてみっちり学習する数学の単元です。ただ、円の勉強といってもここで触れる内容はただ一つです。それは、
円と角度の関係
です。こいつを押さえてしまえばこの単元はクリアしたも同然です。円周上の角(円周角)や中心と円周上の2点がおりなす角(中心角)の関係。これに関する性質がじゃんじゃん登場します。円の公式をまる暗記することも大切ですが、忘れないでほしいのは、
なぜその性質がいえるのか
を検証することです。数学の教科書で語られているすべての「性質」には理由があります。なぜ? なぜ?? なぜ???という問いかけを忘れずに読み進めていってほしいですね。
三平方の定理
高校受験でかなりの頻度で登場するのがこの「三平方の定理」という単元。
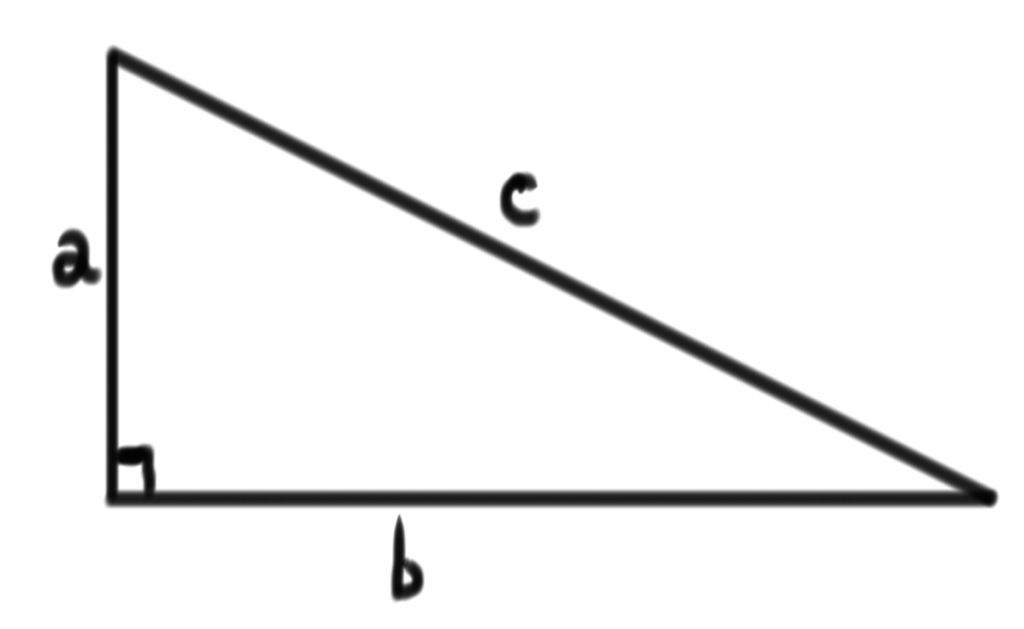
発見者のオッサンの名前にあわせて「ピタゴラスの定理(Pythegorean theorem)」なんて呼ばれたりします。これは直角三角形の3つの辺の関係をあらわした超重要かつシンプルな定理です。たとえば下のような直角三角形の形をしたピザがあったとしましょう。
そしたら、この美味しそうなピザの3つの辺の長さの関係は、
c^2 = a^2 + b^2
となります。これがピタゴラスという男が古代エジプトで発見した直角三角形の定理なのです。こいつを日本ではなぜか「三平方の定理」と呼んでいます。この定理をもちいて、あんなことをしたり、こんなまねをしてみたりするのですね。なるほど。
中学3年生で勉強する「統計学」の数学単元
最後に「統計学(statistics)」の勉強を中学3年時にします。統計学とは、
たくさんの不規則なデータを集めて、ある規則を見いだす学問
のことです。中学1年、2年生では「確率」や「度数分布」などを勉強してきましたね。中学3年生でもちょこっとだけ統計学の分野を勉強していきます。
中学数学の教科書の単元でいえば、
標本調査(Sampling)
という単元です。ここでは、世の中の統計学にもとづいて行われた調査がどのような仕組みで行われるのか、といったことを勉強していきます。
たとえば、テレビ番組の視聴率。テレビは無料でみれますよね? あっ、NHKとか衛星放送をのぞく民放の話ですけど。なぜ民放が無料で視聴できるのかというと、
広告主が広告をだしてお金を払っているから
ですよね。そこでこの「広告主」はなるべく多くの人に自社の広告をみてほしいわけです。
そこで登場するのが「テレビ視聴率」という標本調査。
テレビ局はなるべく全国民のテレビに視聴率調査機をとりつけたいですが、手間と時間と金がかかる。そこである一定数のテレビ視聴者(標本)に協力してもらい、データをとることにしました。
ここでいう「全国民のテレビ視聴状況を確認すること」を「全数調査 (census)」といい、「ある一定数の視聴者をぬきだして調査すること」を「標本調査(sampling)」と呼ぶわけです。
そんなこんなで、標本調査はとても身近で役に立つお勉強です。受験勉強で忙しい時期かもしれませんが、こっそりと勉強しておきましょう!
最後に中学三年生で習う数学の単元をおさらい!
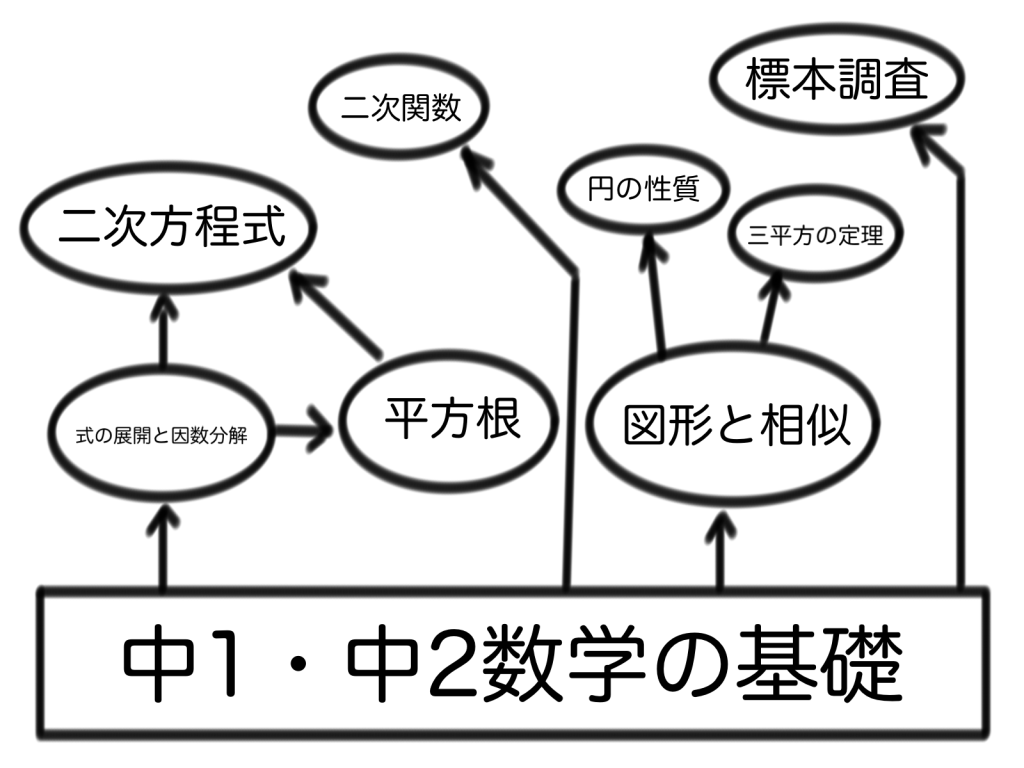
ふう。ここまで8つの数学単元を4つの種類に分類してきました。ここでは最後にもう一度整理して、それぞれの単元ごとの関係性を図で確認しましょう!
この図からもわかる通り、中学三年生の数学は中学1年、2年で学習した内容をもとにレベルアップしてきたものです。
中学1・2年で勉強してきた内容を理解していないと、中学3年生の数学で遅れをとってしまうことになります。決して、中学3年生の数学からまじめに勉強しようとしても借金は帳消しになりませんからね!。
ただ、誰でも数学の基礎さえしっかり理解できれいれば中学三年生の数学だって攻略できます。これから一緒にゆっくり勉強していきましょう。
それでは、また今度です!
Ken