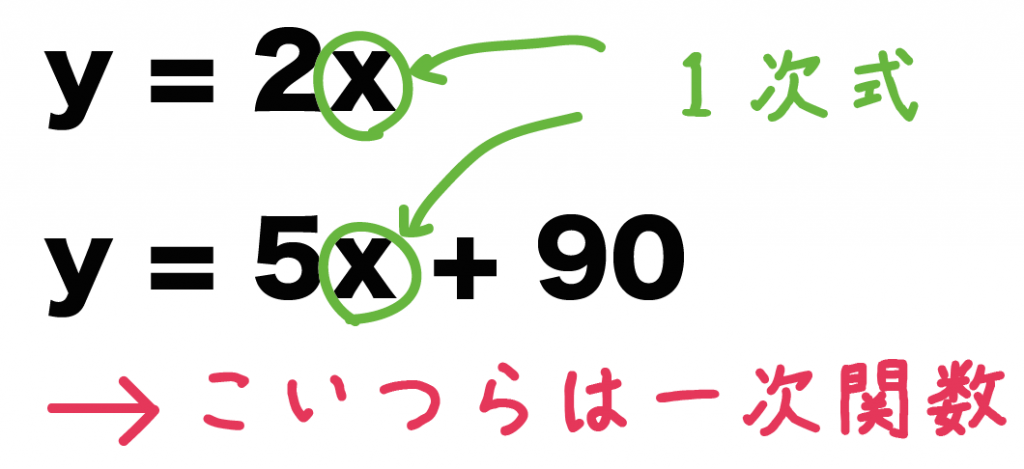反比例って一次関数にふくまれるっけ？？
こんにちは！この記事をかいているKenだよ。コーヒーに牛乳は必須だね。
反比例は一次関数なのか？！？
って思うよね。
教科書には詳しくかいてないし、
ちょっともやもやしてない？？
今日はその疑問を解消すべく、
反比例の関数は一次関数にふくまれるのか？
をわかりやすく解説してくよ。
よかったら参考にしてみて。
反比例は一次関数じゃない！！
結論からいっちまおう。
反比例は一次関数じゃないんだ。
もうね、ぜんぜん違う。
りんごとみかんぐらい違うね。
えっ。
なんで反比例が一次関数じゃないのかって？！？
そうだね。
これから詳しく解説していくよ。
一次関数とはなんだっけ？？
まずは一次関数とはなにか？？
を復習してみよう。
教科書にはこうかいてある↓↓
yがxの一次式で表されるとき、yはxの一次関数である、といいます
だ。
つまり、
関数のxが「一次式」なら一次関数ってことになる。
たとえば、
y = 2x とか y = 5x + 90とかだね。
逆に、y = 2x^2とかy = 5x^3 + 90とかなると、一次関数じゃないってことになる。
だって、xが一次の項じゃないからね。
ここまでオッケイ？？
反比例の式はどうなのよ？？
さっそく本題に入ろう。
それじゃあ、反比例の式はどうなのか。
反比例の式って、
y = a/x
だったよね。xが分母にあるタイプの関数だ。
たとえば、
y = 2/x とか y = 6/xとか。
一見、xは何乗もされていない。
ぶっちゃけ、ただのxにみえるから、
こいつも一次関数じゃん！？
って思うかもしれないけど、そいつは間違いだ。
「一次」って、xを1回だけかけたっていう意味なんだ。
でも、反比例の場合、分母にxがあるから、
xで割っていることになる。
よって、反比例は一次関数じゃないんだよ。
xがかけ算されているのか？
割り算されているのか？
をしっかり見極めるようにしよう。
まとめ：反比例は一次関数じゃないよ！
反比例の式は一次関数じゃない。
これを覚えるだけで大丈夫。
一次関数は慣れれば簡単だから、テストでも点をとっていこう。
そんじゃねー
Ken
