【中学数学】3分でわかる!四分位範囲の求め方〜奇数・偶数対応〜
「四分位範囲の求め方」を教えてほしい!!
こんにちは!竹の妖精ドイサキです。

ドイサキ
中学数学で出てくる「四分位範囲」。
名前からして強そうですよね。
四分位??
範囲??
なにそれ???
しかも問題を見てみると、
- データの個数が奇数
- データの個数が偶数
でやり方が変わるっぽい…。
ってことで今日は、
「四分位範囲の求め方(奇数・偶数)」
を、中学生向けにわかりやすく解説します。
~もくじ~
- 四分位範囲ってなに??
- 四分位数を求めよう
- 四分位範囲の求め方
- データが奇数のとき
- データが偶数のとき
中学数学の「四分位範囲」ってなに??
四分位範囲とはずばり、
データの散らばり具合を表す数
です。
平均との差とはちょっとちがって、
「真ん中の50%が、どれくらい広がっているか」
を見るための指標なのです。
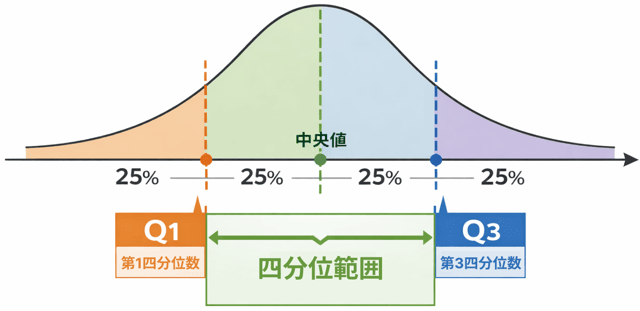
そのために使うのが、
- 第1四分位数(Q1)
- 第3四分位数(Q3)
です。
つまり、四分位範囲を出すには、先に四分位数を求める必要があります。
やることはこの3ステップ。
- データを小さい順に並べる
- 中央値を求める
- 左右に分けて、それぞれの中央値を求める
詳しいやり方はこちらの四分位数の求め方の記事で復習しておきましょう。
四分位範囲の求め方〜奇数・偶数対応〜
四分位範囲の求め方の公式はこれ ↓
四分位範囲 = 第3四分位数 − 第1四分位数
そう、これだけです。
引き算1回です。
たとえば、四分位数の求め方を駆使して頑張った結果、
- 第1四分位数 Q1 = 5
- 第3四分位数 Q3 = 11
が得られたとします。

さて、四分位範囲の求め方は
四分位範囲 = 第3四分位数 − 第1四分位数
でしたね?
この公式にもろもろの値をぶち込んでみると、
四分位範囲
= 11 – 5
= 6
になります。
つまり、四分位範囲は6!
この
四分位範囲 = 第3四分位数 − 第1四分位数
という求め方はデータの個数が奇数だろうが偶数だろうが同じ。
問題は、
第3四分位数と第1四分位数の求め方が偶数と奇数の場合で異なるってことですね。
そこらへんの事情は、さっきからチラチラ登場している四分位範囲の求め方で復習しておいてくださいね。
まとめ:四分位範囲、これで完璧!
はい、四分位範囲は、
- 中央値
- 第1四分位数
- 第3四分位数
が全部つながった用語でした。最後に紛らわしい「四分位数」と「四分位範囲」の違いをおさらいしておきましょう。
| 項目 | 四分位数 | 四分位範囲 |
|---|---|---|
| 意味 | データを4等分するときの区切りとなる数 | 真ん中50%のデータがどれくらい広がっているかを表す量 |
| 種類 | 第1四分位数(Q1) 第2四分位数(Q2・中央値) 第3四分位数(Q3) |
1種類のみ |
| 求め方 | データを小さい順に並べ、 4等分した位置の値を求める |
第3四分位数 − 第1四分位数 (Q3 − Q1) |
| 役割 | データの区切りの位置を知る | データのばらつきの大きさを知る |
| 単位 | 元のデータと同じ | 元のデータと同じ |
| 箱ひげ図での表し方 | 箱や線の区切りの位置 | 箱の横の長さ |
名前は難しそうだけど、やってることはシンプル。言葉に負けないようにしよう!

ドイサキ
そんじゃねー