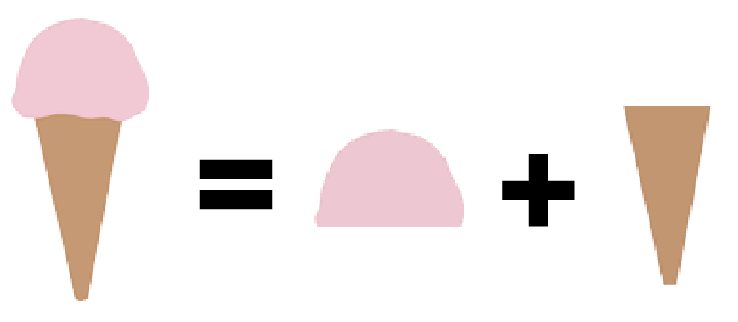半球の体積の求め方に公式はあるの？？
こんにちは！この記事をかいているKenだよ。シャツほしいね。
半球の体積を求め方には公式があるよ。
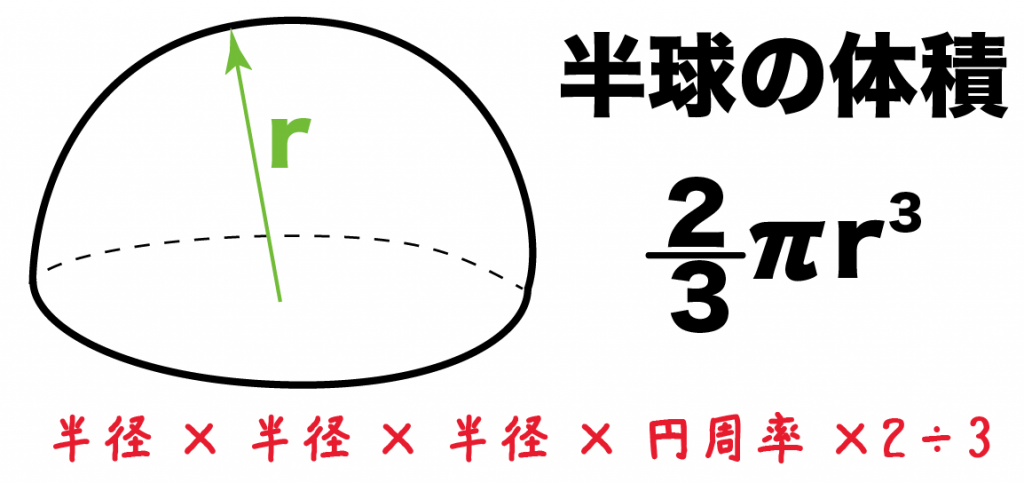
半径rの半球の体積は、
（3分の2π） × （rの3乗）
になるんだ。
つまり、
半径×半径×半径×円周率×2÷3
ってわけだ。
えっ。
覚えられないだって？？！
じつはこの公式。
球の体積のちょうど半分なんだ！
球の体積の公式は、
（3分の4）×（円周率）×（半径）×（半径）×（半径）
だったよね？？
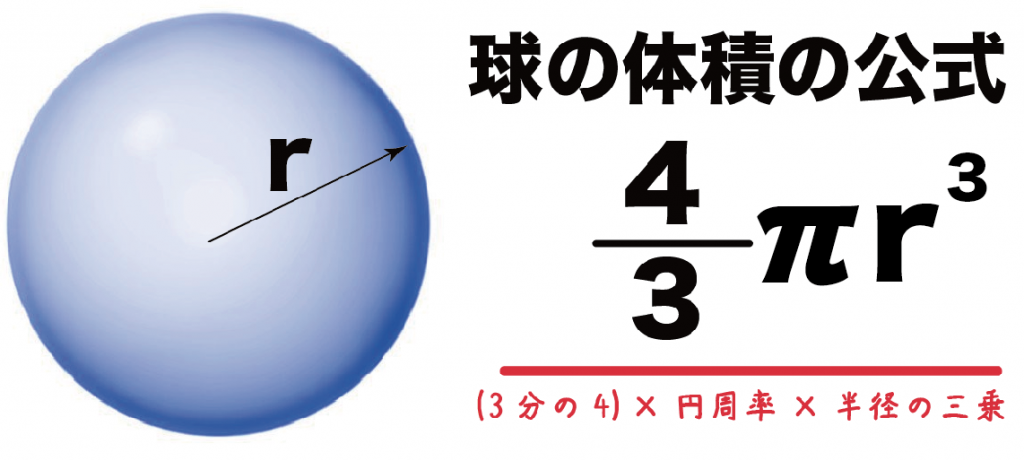
それを半分にしたのが「半球の体積の公式」になる。
なぜなら、
半球は球をスパッと半分にきったものだからね。
体積は球の半分になるってわけ。
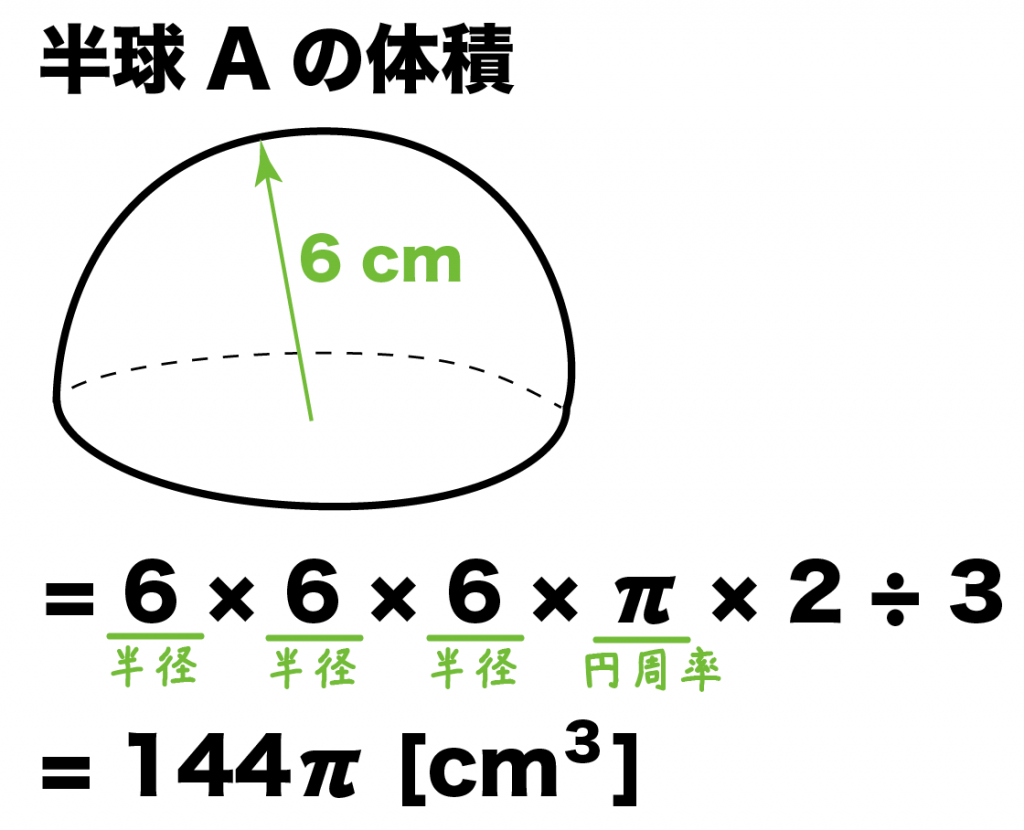
たとえば、半径6cmの半球Aがあったとしよう。
こいつの体積は公式をつかうと、
（半球Aの体積）
=（半径）×（半径）×（半径）×（円周率）× 2 ÷ 3
= 6 × 6 × 6 × π × 2 ÷ 3
= 144π [cm^3]
になるんだ。
どう？？半球の体積を求められたかな？？
半球の体積の求め方の例題をみてみよう！！
半球の体積なんてぜんぜん使わなくね？？
って思ってない？。
ぶっちゃけ、半球をみくびってるよね。
その気持ちわかるw
ただ、半球の体積の求め方は、
立体の応用問題で役に立つんだ。
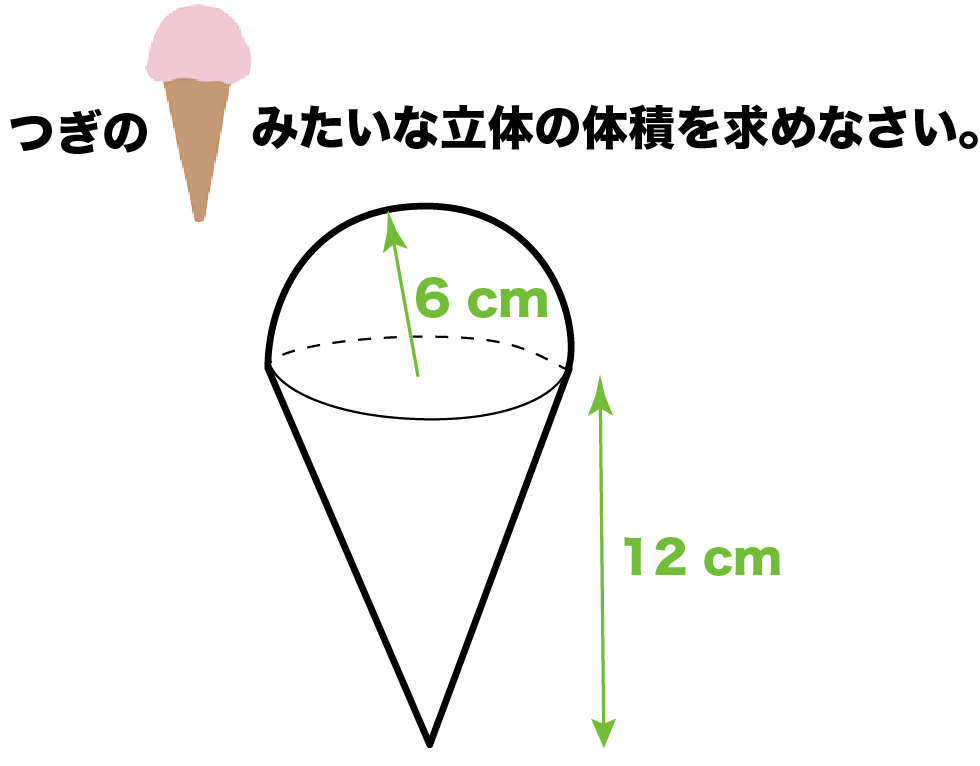
たとえば、つぎのような問題だね↓↓
この問題は3ステップでとけちゃうよ。
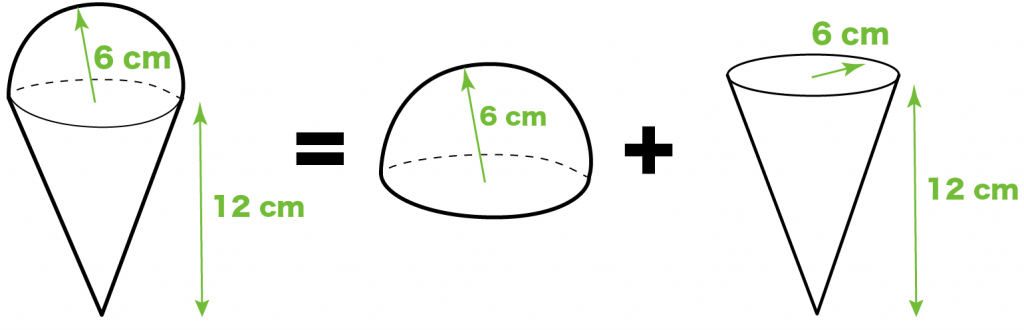
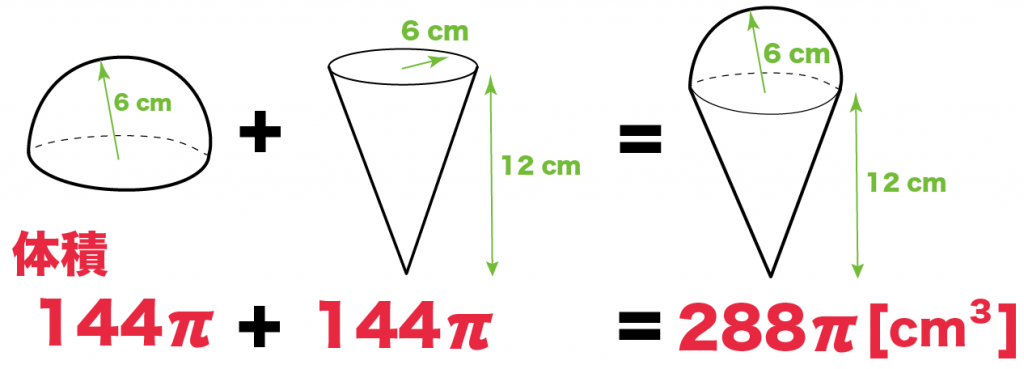
Step1. 「半球」と「円錐」に分解する
まずソフトクリームを、
「アイス」と「コーン」に分解してみよう。
つまり、上の「半球」と下の「円錐」にわけるってことさ。
これが第1ステップ！！
Step2. 体積を計算する！
「半球」と「円錐」の体積をべつべつに計算してみよう！
体積の求め方の公式はそれぞれ、
- 半球の体積： 半径×半径×半径×3÷2
- 円錐の体積： 半径×半径×高さ÷3
だったよね？？
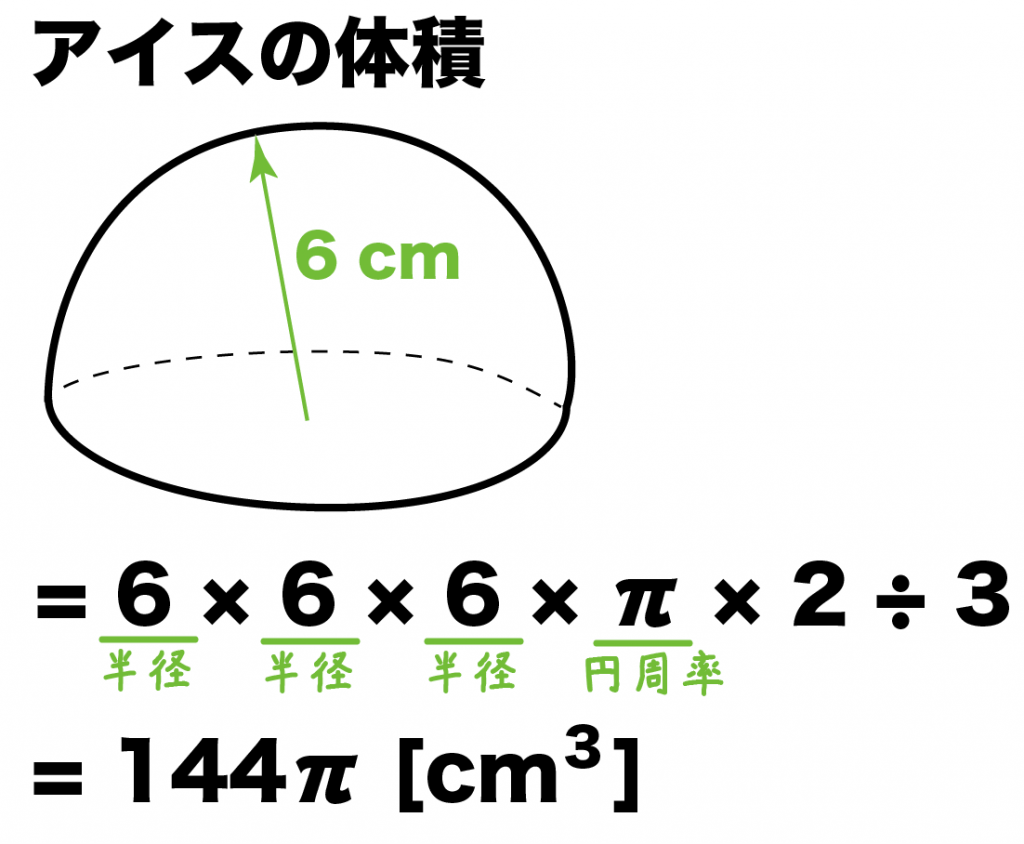
まず半球の体積は、
6×6×6×π×2÷3
= 144π [cm^3]
になる。
半径×半径×円周率×高さ÷3
だったよね？？
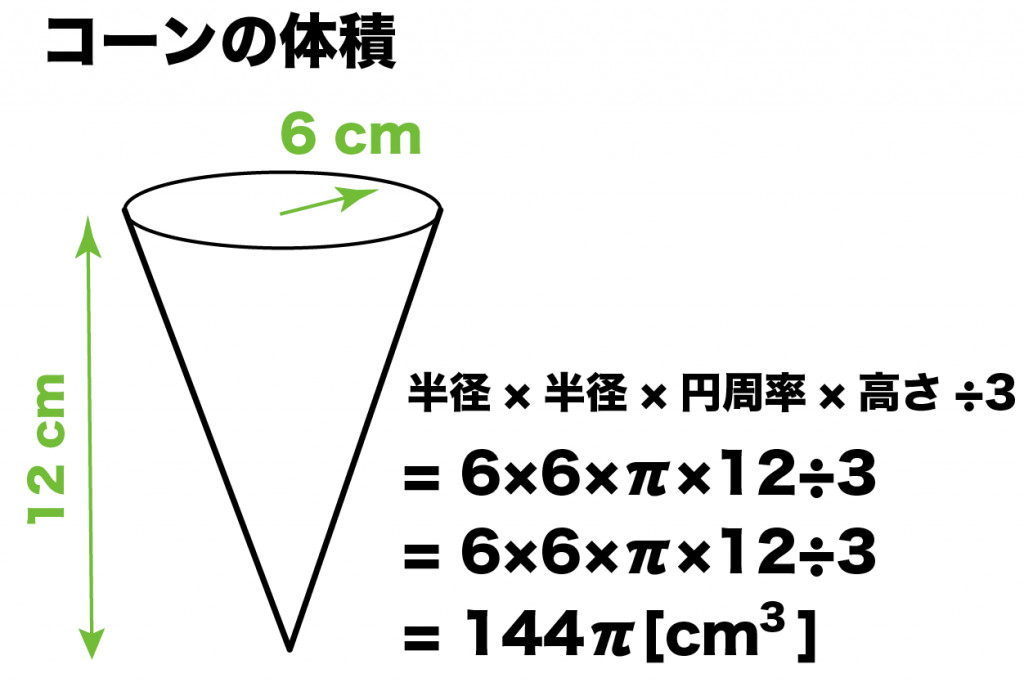
こいつで下のコーンの体積を計算してやると、
半径×半径×円周率×高さ÷3
= 6×6×π×12÷3
= 144π [cm^3]
になるはずだ。
これが第2ステップ！！
Step3. 体積をたす
最後に、
- 半球（アイス）
- 円錐（コーン）
の体積をたしてみよう。
例題での体積はそれぞれ、
- 半球（アイス）：144π
- 円錐（コーン）：144π
だったよね？
こいつらをたしてやると、
ソフトクリームの体積
= （半球の体積）+（円錐の体積）
= 144π + 144π
= 288π [cm^3]
になるね。
おめでとう！
これで応用問題もクリアだね。
まとめ：半球の体積の求め方は役に立つ！！
半球の体積の公式はマイナー。
だけど、覚えておいて損はない。
ソフトクリームみたいな立体の体積もわかっちゃうし。
半球の体積は「球の体積の半分」っておぼえておこう！
そんじゃねー
Ken
