正方形と扇形の面積をつかった問題？？
こんにちは！この記事をかいているKenだよ。ガムはかむほどうまいね。
「正方形」と「扇形」の面積をつかった問題。
たまーにでてくるよね。
たとえば、つぎのような問題だ。
例題
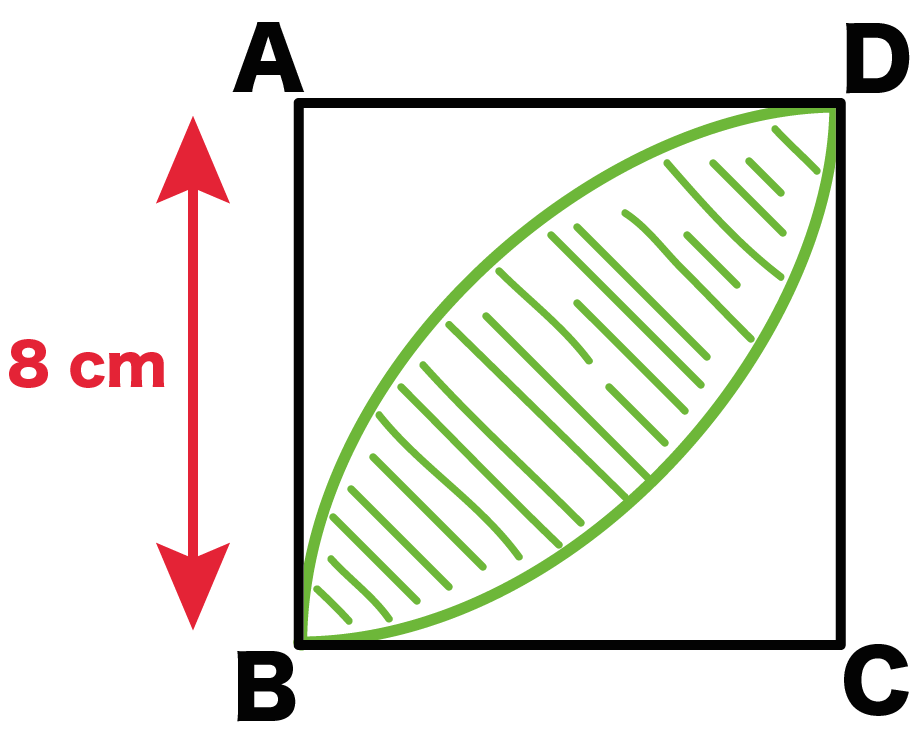
つぎの図形における緑の斜線部の面積を求めなさい。ただし、四角形ABCDは正方形で1辺の長さを8cmとする。
えっ。なんか虫みたい！？
えっ、キモ・・・・
って避けたくなる気持ちもわかる。難しそうだし。。
だけど、解き方をしっていれば、つぎの3ステップで計算できちゃうんだ。
- 扇形の面積を計算する
- 正方形の面積を計算する
- 扇形の面積の和から正方形をひく
正方形と扇形の面積をつかった問題がわかる3ステップ
例題をといてみよう。
例題
つぎの図形における緑の斜線部の面積を求めなさい。ただし、四角形ABCDは正方形で1辺の長さを8cmとする。
Step1. 扇形の面積を計算する！
まず、扇形の面積を計算していくよ。
えっ。
扇形なんてどこにもないって！？？
たしかにね。
だけど、よーくみてみて。
じつはこの図形のなかには、
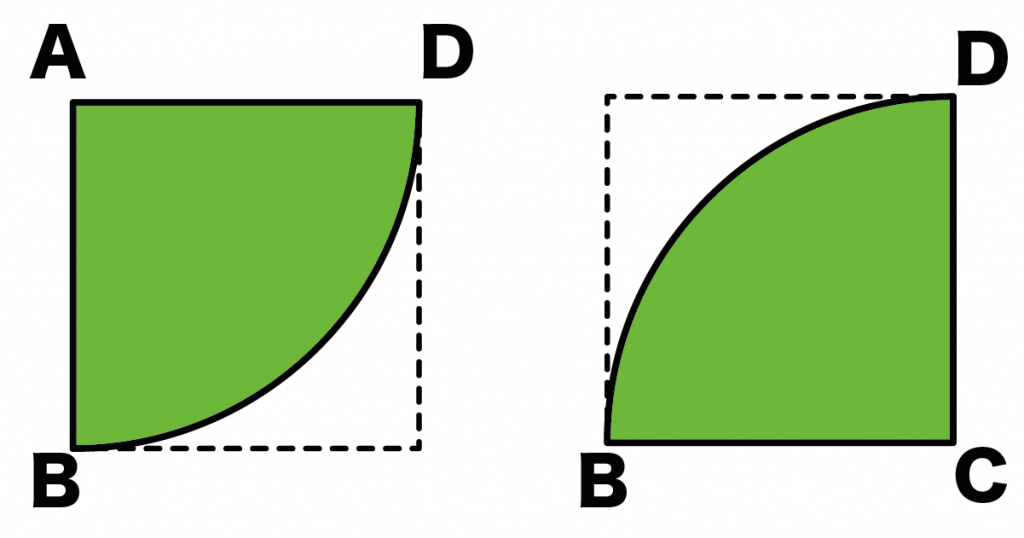
- 扇形ABD
- 扇形BCD
の2つの扇形がかくれているんだ。
それぞれ同じ面積になっているね。
計算してやると、
扇形ABD = 扇形BCD
=半径×半径×中心角÷360
= 8 × 8 × 90°÷360
= 16 [cm²]
になる！
Step2. 正方形の面積を計算する！
つぎは、正方形の面積を計算していくよ。
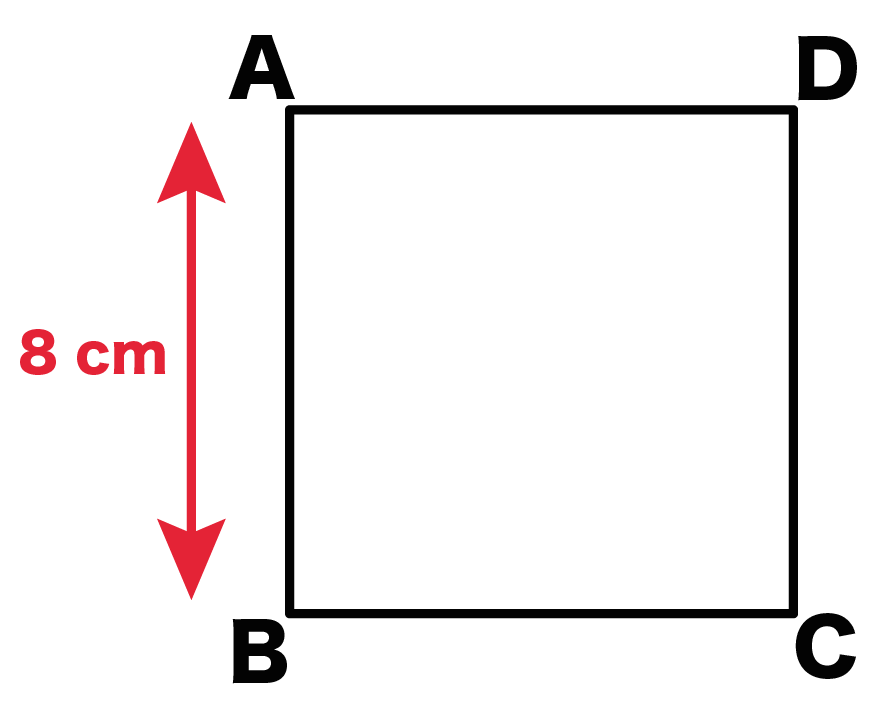
例題でいうと、正方形ABCDだね。
（正方形の辺の長さ）×（正方形の辺の長さ）
だったね？
ってことは、正方形ABCDの面積は、
8× 8
= 64[cm²]
になるんだ！
Step3. 「扇形の面積」をたして「正方形の面積」をひく！
いよいよ最後の仕上げ。
「扇形の面積」をたして「正方形の面積」をひいてみよう。
例題でいうと、
- 扇形ABD
- 扇形BCD
をたして、正方形ABCDの面積をひけばいいんだ。
だから、
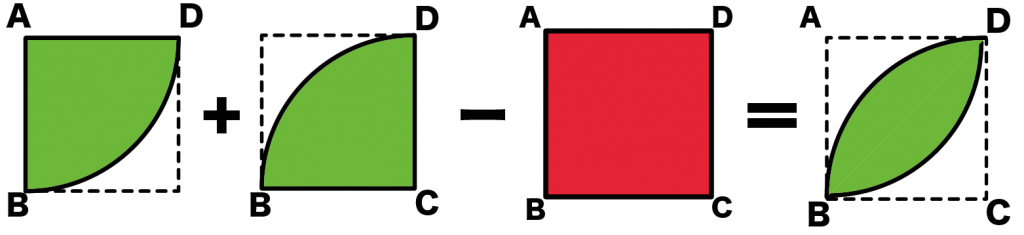
（扇形ABD）+（扇形BCD）-（正方形の面積）
= 16π + 16π – 64
= 32π – 64 [cm²]
になるね。
どう？？計算できたかな？？
まとめ：扇形の面積をたして正方形の面積をひこう！
「扇形の面積」をたして、
「正方形の面積」をひけばいいんだ。
いろいろな問題にチャレンジしてみてね。
そんじゃねー
Ken
