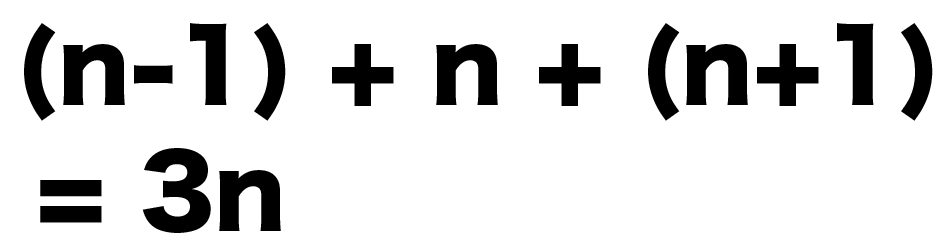連続する3つの整数の和が3の倍数になるってほんと！？
こんにちは！この記事をかいているKenだよ。おしぼりは無敵だね。
文字式の利用で、
連続する3つの整数の和の問題
ってでてくるよね。
たとえば、つぎの問題 ↓↓
例題
連続する3つの整数の和が3の倍数になる訳を説明しなさい。ただし、整数は正の数とする。
日常生活では3つの整数の和なんて考えないよね？？
だって、必要ないもん。
でもね、中2数学の問題ではよくでてくる証明なんだ。
今日はこの問題を攻略してみよう！
連続する3つの整数の和の証明がわかる4ステップ
4ステップで証明できちゃうよ。
- nを整数とする
- 連続する3つの整数をnであらわす
- たす
- さけぶ
さっきの例題をといていこう！
例題
連続する3つの整数の和が3の倍数になる訳を説明しなさい。ただし、整数は正の数とする
Step1. 整数をnとする
ある正の整数を「n」としてみて。
nは「正の整数」だから、
1にもなるし、2にもなるし、10にだってなるんだ。
えっ。なぜ「n」を使わなきゃいけないんだって？！
えっ？
zを使いたい？？
じつは、nは英語の「number (数字)」からきているんだ。
ぶっちゃけzとかqでもいいんだけどさ。
nをつかうとカッコいいじゃん？。
とりえあず正の整数を「n」とおこう！
Step2. 連続する整数をnであらわす
連続する3つの整数をnであらわそう！
連続する3つの整数ってたとえば、
1, 2, 3
みたいに、1ずつ違う整数のことだ。
たとえば、
1, 4, 5
とかは連続してないね。
だって、1ずつ離れてないし。
nであらわすときは、
連続する3つの整数のうち、正の整数nを、
真ん中の整数
とおくといいよ。
そうすると、
- 一番小さい整数
- 一番大きい整数
をnで簡単にあらわせるからね。
連続する3つの整数は1ずつ離れてる。
よって、
- n-1
- n
- n+1
になるはずだ！
Step3. たす
つぎは、連続する3つの整数をたそう。
nであらわした、
- n-1
- n
- n+1
をたせばいいんだ。
ぜんぶたしてみると、
(n-1)+n+(n+1)
= 3n
になるね！
Step4. 和が3の倍数になると証明する
最後に、和が「3の倍数」になる証拠をみつけよう。
証拠がみつかれば、
連続する3つの整数の和が「3の倍数」である
って証明できるからね。
例題でいうと、
連続する3つの整数の和は、
3n
になったね。
で、nは正の整数だったよね？？
ってことは、
3n
は3の倍数になるんだ！
だって、「n」には1とか2とか6とかがはいるわけだからね。
そいつらが3倍されたら、
- 1→3
- 2→6
- 3→9
3の倍数になるじゃん？？
だから、連続する3つの整数の和は3の倍数っていえるんだ！
まとめ：連続する3つの整数の和は3の倍！
この問題は、
- 正の整数をnであらわす
- 連続する整数たちをnであらわす
- たす
- さけぶ
の4ステップで証明できちゃう。どんどんチャレンジして行こう
そんじゃねー
Ken
