【中学理科】3分でわかる!力の合成と分解を作図する方法

おっす!パンダの妖精・月縄だ!
今日は、力の合成と分解の作図をマスターしようぜ。
今日は、力の合成と分解の作図をマスターしようぜ。
力の合成の作図方法
力の合成っていうのは、
2つ以上の力を1つにまとめる方法のこと
だったよな。
直線上にある2力の合成
おっし、まずは合成する力たちが1つの直線上にある場合からいくぞ。
力Aと力Bが同じ方向に向かっているなら、その合力はシンプルに2つの力を足し合わせたものになる。
力Aの大きさがa、力Bの大きさがbなら、合力Fは、
$$ F = a + b $$
だ!
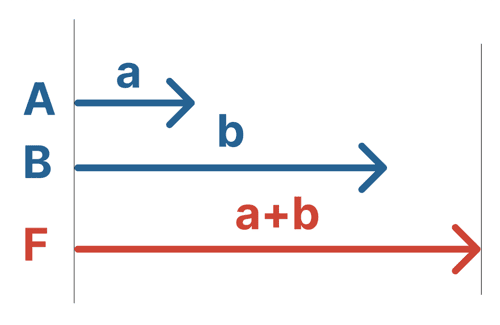
力の向きはもちろん、もとの力たちと同じだぜ。
たとえば、力Aの大きさが3、力Bの大きさが2なら、合力Fは、
$$ F = 3 + 7 $$
$$ F = 10 $$
になるってこったな!
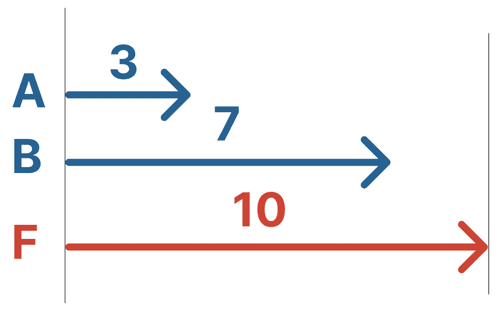
直線上にない2力の合成
次は、直線上にない2つの力の合成だ。
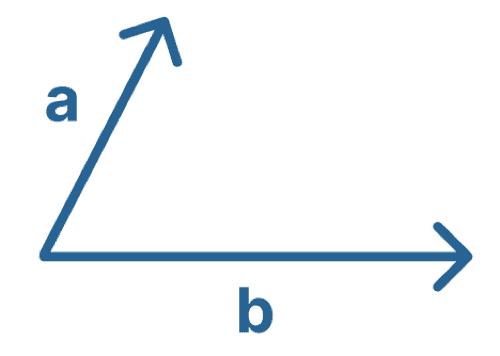
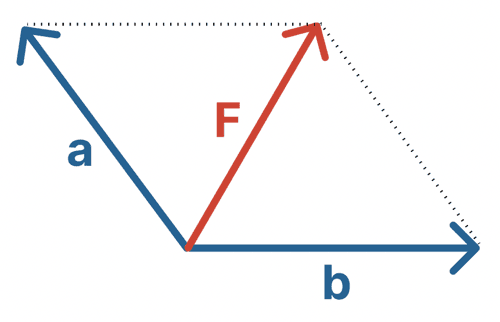
ここでのポイントは、平行四辺形を使うことだ。力Aと力Bをそれぞれの辺とする平行四辺形を描こう。
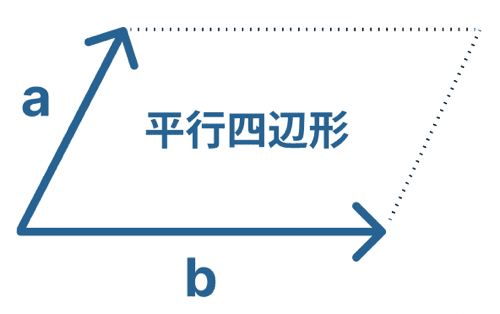
すると、その対角線の向きが合力の向きになるんだ。
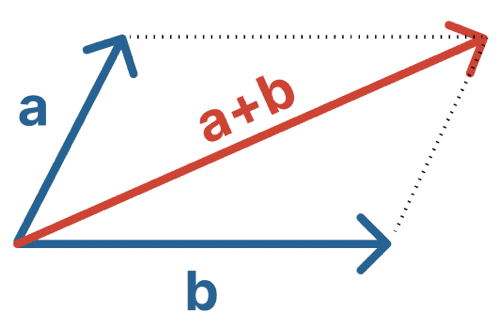
合力の大きさは、その対角線の矢印の長さとして表される。
これを作図で確認しよう!
力の分解の作図方法
力の分解とは、
ひとつの大きな力を2つ以上の力に分けること
だったよな。
作図のポイントは次の通りだ。
- 力を分解する方向を決める。
- 力を平行四辺形の対角線にしよう。
- 平行四辺形の他の二辺が、それぞれ分力になる。
たとえば、こんな感じの力Fがあったとする。
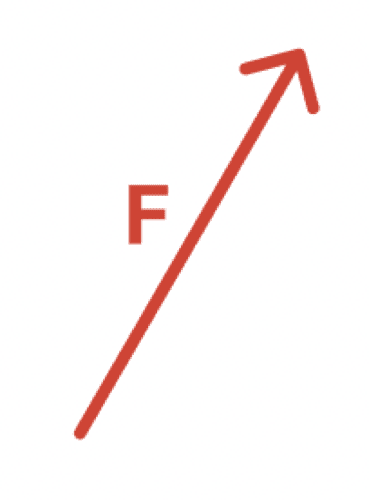
まずは力を分解する方法を決める。分解する2つの方向を決めてくれよな。
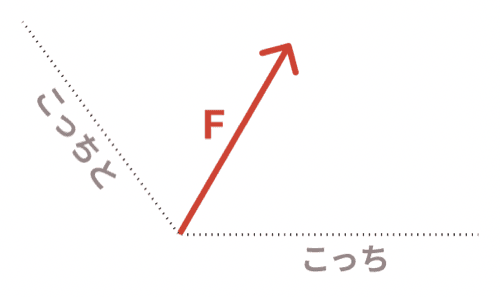
で、その2つの方向でFが対角線になるような平行四辺形を書く。
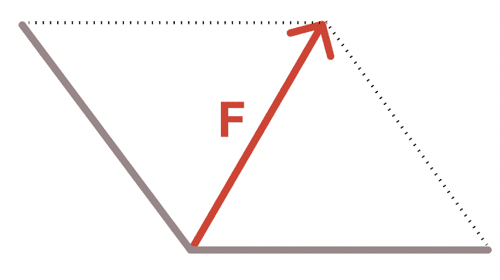
このとき、平行四辺形の2辺が分解した分力になるってことよ。

これで力の合成と分解マスターだ!
しっかり復習して、どんな力も味方につけようぜ!
しっかり復習して、どんな力も味方につけようぜ!



