こんにちは!この記事を書いているKenです。昼飯に焼き肉を食べました。
分配法則 (distributive property) という計算法則をご存知ですか?! 名前が超カッコイイこの法則は、中学1年生の数学でで登場します。
はじめてこの数学用語をみかけた中学生の方は、
は?? 分配??? お、おれの財産は渡せねえよう!
とぶっきらぼうになってしまうかもしれません。そんな一見、超うさん臭い「分配法則」くんですが、じつは中学校の数学の中で、かなりかなりの重要度を誇っています。
分配法則さえマスターすれば中学1年生の数学の大半を倒せます。中学1年生から数学の問題を倒せる武器を所持できるなんてうらやましいですね、まったく!

分配法則という武器を使いこなせ!!
今日はせっかくなので、
分配法則という最終兵器の概要を説明しながら、あまり知られていない便利な使い方まで紹介していきます。
分配法則の使い方がわからなくて悩んでいる方は参考にしてみてくださいね。
分配法則をわかりやすく説明してくれたら欲しいものあ・げ・る
と美女に迫られたとしましょう。なんとしても欲しいものを手に入れたいぼくは、分配法則を次のように説明するかもしれません。それは、
分配法則とは、たし算とかけ算の橋渡しの法則のことだね。
と。たぶん、こんなきざな台詞を使えば、美女も・・・・・
なんて妄想はさておき。なぜ分配法則が「たし算とかけ算の橋渡しの法則」になるのか確認していきましょう!
分配法則は中学数学の教科書で以下のように説明されています。
a, b, cという3つの数字による計算式があったとしましょう。分配法則を使うとこの文字式は次のように書き換えることができます。
$$a\times(b+c)=a\times b+a\times c$$
です。えっ。文字ばっかりで分かりづらいですって?!? そんな方のために実際の数字で分配法則を考えてみましょう。上のa, b, cを4、5、6という数字で置き換えてみると、
となります。
左の計算式を右のようにべつの形で書き換えられるわけです。このように左辺から右辺に式を変更することを分配法則を使っちゃる、といい、ちまたでは「カッコをはずす」なんて異名で呼ばれています。
まとめると、
計算式の()をなくせる法則を「分配法則」と呼んでいるわけです。
分配法則が便利なケースっていったいどんな場合でしょう??
さっきの説明では全然分配法則が役に立つ気配ありませんよね??? むしろ足を引っ張っているような気がします。
たとえば、先ほどの例であるでは余計に左辺の式を複雑にしています。なんだろう、このままでは分配法則なんて消え失せろなんて言われそうです。
そこで、読者の方が分配法則に惚れ直すことを願い、分配法則がむちゃくちゃ効力を発揮しているケースを紹介していきます。
分配法則が役に立つケースの1つとして挙げられるのは、
「桁数の大きい数字」×「1ケタの小さい数字」という計算
です。たとえば、
のような計算式。この2ケタ×1ケタ数字のかけ算は、そろばんを習っていないと瞬殺できません。ぼくはそろばんを習っていないので、この計算を終了させるのに5分ぐらいかかりそうです。えっとお、小学校で勉強した筆算の方法を利用して、

なんて感じです。じつは小学校で勉強した通りに筆算の公式を利用せずとも、この計算を瞬殺する方法があるんです。それは、
分配法則をつかって桁数の大きい数字をばらしてあげる
という方法です。えっ? どういうことなのか意味不明ですって!??
それでは詳しくわかりやすく説明していきましょう。
まずは桁数の大きい数に注目します。という計算式でいえば、
がそれに値します。
このときのポイントは、
きりのいい桁数でわけわけする
ことです。つまり、14の場合ですと、10がきりのよい桁数です。14を「10と4が足された数字」と捉え直してやるわけですね。
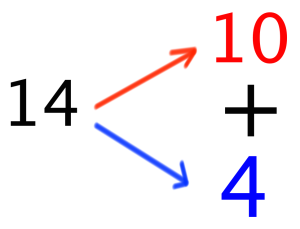
すると、という計算式は、
という()を含む計算式に変化させることができます。
桁数の大きい数字をたし算の計算式に変換したら、分配法則の出番です。記事の初めで学んだ「分配法則」をつかって式中の()をはずしてやると、
となります。え?余計に計算過程が増えてしまったですって!?? た、たしかにその感は否めません。だがしかし、の前の項の
という計算はえらくカンタンです。なぜなら、10を7にかけるだけですからね。すると、
と答えを導くことができます。14を(10+4)に変形して分配法則で()をはずす。これだけで難しい桁数の大きいかけ算もとけることになります。
この分配法則の活かし方は桁数が増えても同じです。たとえば、といった具合にです。この3ケタと1ケタのかけ算にも分配法則を適用してやると、
という感じになります。やりましたね!
それじゃあ、なぜぼくは分配法則を「橋渡し法則」と呼んでしまったのでしょうか!? さっきまでの説明に橋なんて1個も登場しませんでしたね。これじゃあ、嘘をついた罪で逮捕されそうです。
先ほどの計算式をよーーく見つめてみてください。
これです。これ。
この数式を長いこと見つめていると、
分配法則により、かけ算が足し算になったり、足し算がかけ算になったりしている、
ということが分かります。
14という数字を(10+4)というたし算の形にしたり、を
という足し算とかけ算が混じる計算式に変換したりと大忙しです。ま、まさに、分配法則は「たし算とかけ算の橋渡し法則」ですね!
それでは、また今度です!
Ken
中学数学の最初の単元「正の数・負の数」で2つの計算法則が登場します。
それは、
交換法則 (commutative property)と結合法則(associative property)
です。数学を勉強しはじめた中学生のたちは、
交換? 結合?? 法則とかうさんくせえー
なんて不平をもらし、数学を嫌いになってしまうかもしれません。

数学が嫌いになりそうになったので、Wikipediaで結合法則の意味を調べてみると、
数学、殊に代数学における結合法則(けつごうほうそく、英: associative law) 、結合則、結合律あるいは演算の結合性(けつごうせい、英:associativity)は二項演算に対して考えられる性質の一つ。ひとつの数式中で演算が一度よりも多く行われるとき、その演算を評価する順番に関わらず結果が同じになるような演算は結合的 (英: associative) であるといわれる。
と書いてあります。余計に意味不明で泣きそうになりますよね、コレ。
そこで今日は数学を勉強し始めた中学生の方でもよくわかるように、
交換法則と結合法則の使い方
を説明します。交換法則とか結合法則の意味がわからなすぎて泣きそうになっている!??
そんなときに参考にしてくださると嬉しいです。
まずは最初に「交換法則」の正体を暴いていきます。交換法則とはずばり、
計算式に含まれる項の順序を入れ替えていいよ!
という法則です。したがって、項の数が2つ以上の計算式から「交換法則」を適用できるわけです。たし算(加法)とかけ算(乗法)の2つの場合に適応できることが知られています。
たとえば、
という計算式があったとしましょう。この文字式に交換法則をあてがってやると、
という具合に計算順序をかえてもいいんです。これは加法の場合の交換法則です。教科書では俗に「加法の交換法則」と呼ばれています。
えっ。乗法の交換法則の例もみてみたいですって!??
そうですね、先ほどの足し算の記号+を×に直して、
という計算式をつくってやれば、乗法の交換法則の出来上がりです。
計算式の項の順序をいれかえても加法・乗法の計算結果は変わらない
という法則が交換法則です。わかりやすいですよね!??
それでは、もう一つの計算法則である「結合法則」とはいったい何者なのでしょうか。
先ほどWikipediaでの結合法則の意味を確認してみましたね。ただ、あの定義は難しすぎて数学を猛烈に勉強した人にしかわかりません。
そこで改めてここで「結合法則」を再定義してやると、
3つ以上項がある計算式で、どのペアーから計算しても構わないYO!!
というものです。この「結合法則」は「交換法則」と同様に「たし算とかけ算」の2つの場合に適応することができます。
し、しかも項の数が3つ以上?? なんだかうさんくさい数学の法則ですね。具体例といっしょに理解を深めてみましょう。
たとえば、
という計算式があったとします。3つも項があるので厄介な計算式です。
ふつうに何も考えずに計算すると、まずを計算して、その答えに-5をかけて…..
という計算をするでしょう。
つまり、
のように無意識に前の2つの項を()でくくっています。
ただ、という計算はそろばんを習っていない限り瞬殺できません。これではクラスの数学が得意なライバルたちに差をつけられてしまいます。
そこで登場するのが「結合法則」です。結合法則を適応してやると、
という計算式の
を先に計算したっていいことになります。つまり、
のように後ろ2つの項をくくっても良い訳です。
この計算をすると、だということがわかります。
そして、この20という数値に第一項の9をかけて、
という計算をすることになります。これは先ほどの
という計算式と比べるとかなり楽勝になっています。だって、20ってきりのいい数字ですからね。そろばんを習ってなくても答えは、
と導くことができます。一見、複雑な計算式をカンタンにできる。これこそが結合法則の武器です。
先ほど紹介したのは「乗法の交換法則」です。かけ算の場合ですね。この結合法則は足し算(加法)の場合にも適応できます。足し算の計算式でも臆せずじゃんじゃん使って行きましょう。
それじゃあ、ここまで勉強した「交換法則」と「結合法則」を抱き合わせるとどんなことが分かるのでしょうか??
じつは交換法則と結合法則から、
加法・乗法の計算式では、どの項から計算してもいいし、どの項同士をくっつけてもいい
ということが言えます。つまり、自分が計算しやすいように項を自由に動かしていいのです。かつてフランス革命によりフランス国民に自由が与えられたように、「交換法則と結合法則」によって中学生に計算の自由が与えられたわけです。
ただし、ここで1つ注意点があります。
加法と乗法(たし算とかけ算)が混じった計算式では、
カッコ内の計算→乗法→加法
という計算順序があります。十分に注意して取り組みましょう。
最後に実際に「交換法則」と「結合法則」を利用して計算問題をといてみましょう。
見た目がかなりごっつく厳つい顔をしています。交換法則と結合法則を使わなかったら返り討ちをくらいそうな勢いです。
このモンスターを退治するために、さっそくモンスターを倒してみましょう。
どうやらこの式を眺めていると、
をしてしまえば、89という端数が消えて計算がカンタンに成りそうな気がします。しかも、残りの2つの項だって足せば丁度いい数になりそうな気がします。そこで、まず交換法則を用いて、
という具合に計算順序を入れ替えます。次に、結合法則により、 前後の2つの項のカップルをくっつけ合わせると、
という計算式になります。シンプルになった計算式を根性で計算してみると、
という解が得られます。これは前から順番通りに計算していた頃よりかなり計算過程が楽でしたよね?? その理由としては端数が消えるように「交換法則」と「結合法則」を使ったからです。
この計算式も見た目がかなりごっついですね。 光の速度でこの問題をとくために、交換法則と結合法則をつかってやりましょう。
まず、交換法則を使って計算の順番を入れ替えます。なぜなら、8134というモンスターを倒す前にというきりが良さげな計算をしたいからです。
交換法則をつかうと、
という計算式に変化します。結合法則を利用して計算を進ませてやれば、
という答えを抽出できます。ね?カンタンになりましたよね!?
ここまで紹介してきた「交換法則」と「結合法則」はいかがだったでしょうか?!?数学の教科書ではちらりと一瞬しか2つの法則を紹介していません。ただ、例題で分かる通り、
交換法則と結合法則を使えば計算問題がカンタンになります。
まるでその様子はドラえもんのスモールライトのごとく。交換法則と結合法則という2つの道具を難しい計算式にあててやれば、小さくなってしまいます。しかも交換法則と結合法則はドラえもんがいなくても使えちゃいます。 22世紀まで待たなくて済みそうですね。
それでは、また今度です。
Ken
正の数・負の数の基礎をみっちり学びましたか!?? マイナスという新しい数学の概念。絶対値という想像しにくいアイデア。さらには数直線の使い方などを学習してきました。
これで中学数学の勉強でスタートダッシュを切れたも同然です。バナナにひっかからないように、中学数学の勉強をつづけてテストでいい点数をとってしまいましょう・・・・

ところが、です。
正の数・負の数の山場は「正負の数の計算」です。ここまで丁寧に基礎を固めまくってきましたが、それを使わねば話になりません。いわゆる宝の持ち腐れというやつです。
正の数・負の数の四則演算、つまり、たし算・ひき算・かけ算・わり算をマスターしなければ、中間テストで良い得点をたたき出すことはできません。
そこで今日は、正負の数の四則演算で使える問題解法のコツを、
加法(たし算)・減法(ひき算)・乗法(かけ算)・除法(わり算)
の4つの場合にわけて解説していきます。これから中間テストをむかえる中学生の方や、正の数・負の数の四則演算に苦手意識をもった方なんかが参考にしてくださると嬉しいです。
せっかくなので、加法・減法・乗法・除法の順番に計算のコツを紹介していきます。
正負の数の「加法(たし算)」で使える計算のコツは大きく分けて2つあります。これらのコツは、
正負の数の計算が「同符号」のものか「異符号」のものか分類する
ことがベースになっています。
1つ目の場合は、
同符号の正負の数の計算です。正の数・負の数の計算の中でもっともベーシックなタイプの問題です。
えっ。ちょうよくわからないですって!? 具体的な正の数と負の数の計算問題を確認してみましょう。たとえば、
正の数+正の数
負の数+負の数
という計算があったとします。これは加法を行う項が同じ符号なので「同符号」の正負の計算と呼びましょう。この場合、
絶対値の足し算をしてから符号をつけたす
という計算手段をとります。たとえば、
という計算問題があったとしましょう。これは負の数同士の「同符号」の足し算ですので、「符号は無視して絶対値の足し算」をします。(-2)と(-3)の絶対値の和は5ですので、そのあとに負の符号である-をつけたしてやると、
という計算結果がえられます。これで同符号の正負の数「加法」はマスターしましたね!
それでは、「異符号」の正の数・負の数の足し算はどう計算するのでしょうか?? 異符号同士の計算といえば、ちょうど次のようなものです。
正の数+負の数
負の数+正の数
これは先ほどの「同符号」の場合の計算よりも少々やっかいです。なぜなら、
という3ステップを踏まなければいけないからです。
ちょっとこれではよく分かりませんね?? 足し算なのに引き算?? ふざけんなああ!
なんて罵声が聞こえてきそうです。
わかりやすい計算例を出しましょう。たとえば、
という計算問題があったとします。先ほど説明した手順に沿って計算しようとしてみると、
という感じで答えが算出されました。手順を書き出してみるとかなり複雑ですね。 頭がこんがらがってはげてしまいそうです。こんなもやもやとして頭をスッキリさせてくれるのが、
数直線
というアイテムです。数直線を使えば、絶対値がどうとか符号がああーとか関係ありません。ものの3秒で「異符号」の加法問題をとけます。よかったですね!
数直線をつかった解法が気になる方は「【数の大小】数直線を使いこなす3つメリット」という記事を参考にしてみてくださいね。
つづいては正の数・負の数の「減法(ひき算)」の計算問題のコツの紹介です。
減法で使える計算のコツはただ1つ。
それは、
負の符号(マイナス)の後ろの符号が変化する!!
ということです。具体的には以下の2ステップを踏むことになります。
このコツに加えて先ほど紹介した「加法」の計算問題をとくコツを混ぜ合わせてやればもう怖い者なしです。例題をまじえて確認してみましょう。
たとえば、
という正負の数の計算問題があったとしましょう。ここで気をつけたいのは、真ん中の「マイナス記号」の後の(-29)の符号が変化することです。そして、後ろの数の符号を変化させたマイナス記号は+記号に変化します。
したがって、
という計算結果になるわけですね!なるほどなるほど、後ろの数に符号の変化を与えた「マイナス記号」は効力を失い、+の符号にもどってしまうという訳ですね。
これで正の数・負の数の減法の計算をマスターしました!
つづいては「かけ算(乗法)」の計算問題のコツです。ここでも先ほど同様に一つしか計算問題のコツがありません。それは、
乗法の中に含まれる「負の数」の数に注意する
ということです。えっ。負の数の数の何に注意すればいいのか分からないですって?!?
じつは、乗法の中の負の数の数が「奇数」なのか「偶数」なのかの2つ場合によって、計算結果の符号が異なるのです。
ということになります。理解を深めるために実際の例題を確認しましょう。たとえば、
という計算問題があったとします。この乗法の計算式の中に含まれる「負の数」を数えてみると、
2つ!!
であることがわかります。
2という数は「偶数」です。
よって、計算結果は「正の数」になりますので、プラスの符号を計算結果につけてやればいいいのです。
すると、
という答えを導くことができます。正の数と負の数が入り交じった乗法の計算式をみかけたら、まっさきに式の中に含まれる「負の数」の数を数えてくださいね。
お次は「除法」、つまり正の数・負の数の「わり算」です。
基本的には先ほど取りあげた「乗法」と同様に、
式に含まれる「負の数」の数をカウントすること
が大事です。それによって計算結果の正負の符号が決定します。ただ、除法をふくむ計算で気をつけなければならないこともあります。それは、
ある数の除法は、その数の逆数の乗法であること
です。つまり、逆数を用いてやれば除法は乗法と同じことなのです。もう小学校のときのように「かけ算はかけ算、わり算はわり算」というように分け隔てる必要はありません。一緒くたに考えることができます。
たとえば次のような正負の数の計算問題があったとしましょう。
ある数の除法はその数の逆数の乗法に等しい、
ということを利用してこの計算式を書き直してみると、
となります。わり算の計算記号が消えてかけ算になりました。これは超らくちんですね!
除法の場合も乗法の計算の符号ルールが適応されます。この計算式に含まれるマイナスの符号は偶数であるため、計算結果は「正の数」ということになります。よって、この計算問題の答えは、
となります。逆数をつかってやれば割り算がいらなくなります。いいですね、これ!
さて、それでは「たし算」「ひき算」「かけ算」「わり算」の4つを混ぜっこにした計算問題はどうすればいいのでしょうか!??
このまぜまぜになって計算問題を数学の世界では「四則演算」と呼んでいます。なぜなら、「加法・減法・乗法・除法」の4つを合わせて「四則」と呼んでいるからです。ちょっとかっちょいいですね。
じつは、正の数・負の数の計算問題で気をつける「四則演算」の計算のコツは次の1つしかありません。
それは、
乗除を計算してから加減を計算する
というものです。つまり、「かけ算・わり算」を先に計算してから「たし算・ひき算」を計算すればよいのです。たとえば、
という計算式があったとしましょう。先ほどの計算のルールに従い、まずはかけ算である、
を計算します。
すると、
という加法と減法だけの計算式になります。これを冷静に落ち着いて計算してやれば、
と答えを算出できます。どうです??シンプルでしょ???
ただし一つだけ注意点があります。それは、
()をふくむ四則演算
です。カッコを含む四則演算では【】内の計算を優先させなければなりません。ゆったら、カラオケで割り込みで曲を入れるようなものです。たとえば先ほどの例の式に{}がはさまり、
という計算式を考えてみましょう。すると、{}内を先に計算せねばならないので、
となります。{}がひとつ入るだけで計算結果がぐいぐい違うので注意が必要です!
ここまで紹介した正負の数の計算問題のコツはいかがだったでしょうか?? どれも基本的な学習事項ですので、しっかり押さえて正の数・負の数のテストに臨みたいですね。
何か質問とか不平がありましたらご連絡ください。お待ちしております。
それでは、また今度です。
Ken
中学1年生の数学で、
自然数
がでてきますね?
教科書の自然数の説明をみてみると、
正の整数1, 2, 3, …..を、自然数ともいいます
と書かれています。
ちょっとしっくりこないのでWikipediaをのぞいてみると、
自然数(しぜんすう、英: natural number)とは、個数、もしくは順番(これは正確には有限順序数)を表す一群の数のことである。
とあります。
難しすぎて余計に混乱しますね。
そこで、自然数をシンプルに理解するためにこんな記事を書いてみました。
その名も、
自然数に整数0が含まれないの??
です。
自然数でモヤモヤしている方は読んでみてくださいね。
=もくじ=
まずは自然数とは何か??
ということをみてみましょう。
中学数学のレベルでは、
0を含まない正の整数
と覚えておけばいいです。
たとえば、
1とか、
2とか、
50とか、
100000とかです。
です。
0やマイナスがつく負の数は自然数じゃないってことを頭に刻んでおきましょう。
理由はともあれ、
自然数に整数0が含まれない
って勉強しましたね。
このことを直感的に覚える方法が1つあります。
それは、
指を使って数えられる数が自然数
と覚える方法です。
何人の人間の指を使ったって構いません。
とにかく、人間の手の指で数えられるかどうか??です。
もし、数えられたら自然数、
数えられなかったら自然数じゃない、
って覚えておくといいですよ。
ただ、
指で数える数 = 自然数
ではないことに注意。
あくまでも覚え方ですからね!
それでは、整数の0は自然数なのでしょうか??
さっきの覚え方で試してみると、
ん?
手で数えられない!
数えたいけど、どうしよう・・・
ってなると思います。
もし、テストで、
自然数に0は含まれますか?
ときかれたら、手を広げてみましょう。
もし、指で0を数えられたら自然数、そうじゃないなら自然数ではない、
って覚えておけばいいんです。
せっかくなので、「0」以外の数字で自然数に含まれない数を紹介します。
負の整数は自然数ではありません。
-9や-839や-32といった負の数のことです。
すべての整数が自然数に含まれるという誤解に気をつけましょう。
これも先ほどの覚え方を使えば大丈夫。
マイナスの負の数は指で数えられないですよね??
指を降り立たんでもバンドエイドを貼っても、負の整数を表現できそうにありません。
小学校で勉強した「分数・小数」は自然数でしょうか??
答えは、NO!!
自然数ではありません。
ここでも同じように、
指で数えられるか?
ってことを試してみてください。
どうですか?
指ではどう頑張っても分数・小数を表現することができませんよね?
この自然数の覚え方を使えば、うすうす分数や小数が自然数じゃないってことに気づくと思います。
以上で自然数を見分けるコツは終了です。
覚え方は、
指で数えられるかどうか??
でしたね。
テストで迷ったら手で数えようとしてみてください。
数えられたら自然数、数えられなかったら自然数じゃないはずです。
最後に、つぎの練習問題にチャレンジしてみてください。
練習問題
次の数の中で、自然数はどれですか。3秒で選びなさい
+90, 0.2, -1/4, 5, -0.1, 0, 1556
それでは、また今度です!
Ken
絶対値の意味を理解したけど、問題がイマイチ苦手だ・・・・
絶対値の問題を2秒か3秒ぐらいで解いて女子にモテたい・・・
そんな悩みを抱えていませんか??
絶対値の問題は必ず中学1年生の最初の中間テストで出題されます。絶対値の数学問題をスラスラとけないと他の問題に時間をさけなくなります。ひとによっては、絶対値の問題で頭をひねりすぎて試験時間いっぱいになってしまうかもしれません。
そんな苦しい状況にはまらないためには、絶対値問題の出題パターンをおさえることが大切です。中間テストでいい点数をとって悠々自適に暮らしましょう!

はい。
今日はそんな流れで、中間テストで使える「絶対値の問題を2秒でとくコツ」について記事をかいてみました。テスト勉強で絶対値の問題に苦手意識を持っている方は参考にしてみてくださいね。
中学数学テストで現れる絶対値の問題は2種類しかありません。
ポケモンの数である719種類と比較すると小さい数であることがわかります。
テスト問題をつくる数学の先生ごとに問題の詳細は異なります。厳しい先生は生徒を泣かすような数学問題を練り上げ、いつもニコニコしている優しい先生は思わず。顔になってしまう問題を出題しますよね。??
ただ、絶対値の問題の本質を追い求めると、次の2種類の問題が浮かびあがってきます。
つまり、図で表現するとこうなります。
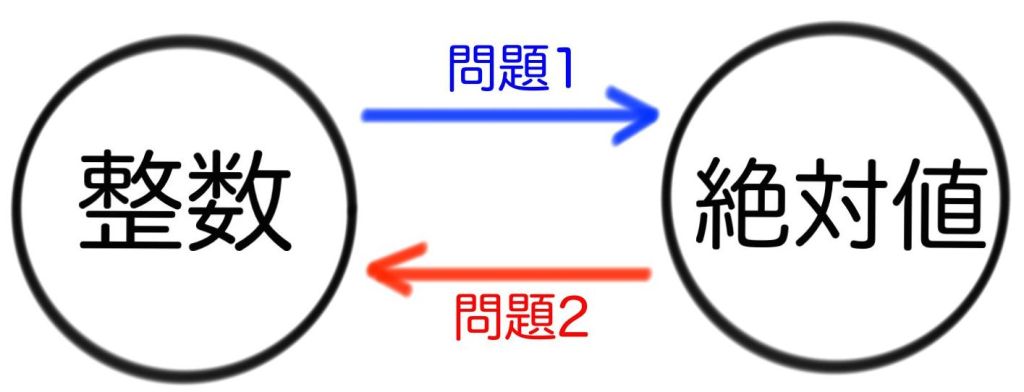
中学数学で出題される絶対値の問題は以上の2つしかないのです。種類が少ないと考えれば、テスト対策も簡単にできますよね。
絶対値の問題をクリアするために、絶対値の問題タイプについて詳しく見ていきましょう!
まずは整数を絶対値になおす問題です。たとえば、-90や-37や+2の絶対値を答えろこらお!といった問題です。ここでの問題解法のコツは、
整数の符号を100%無視する!
ということです。超シンプルですね。
数字の前についてる符号(+か−)をなかったことにすればいいのです。現実世界で人の存在を無視することはイジメになります。だが、しかし、絶対値の問題ではとことん符号くんを無視しましょう。
「整数を絶対値に変換する問題」の具体例として、以下の2つの問題があげられます。
ひとつめの典型的な絶対値の問題は、「○○の絶対値を教えて?ねえ?」という問題。これはむちゃくちゃシンプルな問題です。筆をにぎる瞬発力があればものの2秒で解法できます。
たとえば次のような絶対値の問題があったとしましょう。
次の数の絶対値をいいなさい。
(a) -9
(b) +16
(c)-0.0008
(d) 3/8
ここでぼくらがすべきことは「数字の符号」を無視すること。これだけです。たとえば、(a)の-9でしたら、
数字の前のマイナスの符号を無視して、答えは「9」ということになります。
もし(d)の問題のように「+も−も数字についていないパターン」の場合はどうすればいいのでしょうか??
こういう場合は、問題の数字をそのまま答えてやりましょう!符号がついていない整数は「正の数」ですので、絶対値と実際の整数の値は一致しています。
ちなみに各問題の答えは、
(a) 9
(b) 16
(c)0.0008
(d) 3/8
です。数字の符号を無視するだけ?? とてもシンプルでしょう!?
お次は、無造作に並べられた数字を「絶対値の大小」によって並べかえる問題です。さきほどの問題より複雑そうにみえます。がしかし、やることは(1)の場合と一緒です。冷静に符号を無視しましょう!
例題としてたとえば、
次の数を、小さい方から順に並べなさい。
また、絶対値の小さい方から順に並べなさい。
-0.0008, 0.3, 98, 0, 24, -80
なんて問題があったとしましょう。まずぼくらがやることは「マイナスの符号を無視すること」です。すると先ほどの問題の数たちは次のようになります。
0.0008, 0.3, 98, 0, 24, 80
です。その次は、これらの数字を小さい順に並べ替えてやるだけ、です。すると答えは次のようになります。(左から小さい数字)
0, 0.0008, 0.3、24, 80, 98
となります。やっていることは結構シンプルですね!
これら2つの絶対値の問題のタイプをおさえておけば大抵の絶対値問題をゼッタイにクリアできます。よかったよかった。
2つ目の問題のタイプは「絶対値から整数になおす」問題です。ある絶対値をもちうる整数を答えろごらあ!という問題です。ここでの問題解法のポイントはただ一つ。それは、
ある絶対値をもつ整数は正・負の2つ存在している(0をのぞく)
ということです。

理解を深めるために以下の例題を覗いてみましょう。
絶対値が7以下の整数をすべていいなさい。
この問題でまずはじめにぼくらがすることは、「絶対値が7である整数」を考えることです。「ある絶対値をもつ整数は正・負の2つ存在している」ということに気をつけると、
絶対値7をもつ整数 = -7と7
ということがわかります。これがわかればこの絶対値の問題がとけたも同然。問題が求めていることは「絶対値が7以下の整数」です。7の場合と同様に6以下のケースを考えてみます。すると、
絶対値6をもつ整数 = -6と6
絶対値5をもつ整数 = -5 と5
絶対値4をもつ整数 = -4と4
絶対値3をもつ整数 = -3と3
絶対値2をもつ整数 = -2と2
絶対値1をもつ整数 = -1と1
絶対値0をもつ整数 = 0
となります。ここで注意が必要なのは最後の「整数0」の場合です。整数ゼロは例外で「正負」の2つの整数が存在していません。絶対値0をもつ整数は0しかないという点に気をつけましょう。
すると、この問題の答えはつぎのようになります。
-7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7
の合計15個ですね!
中学数学には大きくわけると以上の2種類しかありません! たった2種類ですよ?? 割り箸を1つ使えば数えられちゃいます。わ、割り箸ですよ?? ものすごくシンプルですね。
中間・期末テストで「絶対値の問題」が出題されそうになったら、この数学の記事を読み返してみてください。きっと、いま取り組もうしている問題が上の2種類のどちらかであるはずです。
それでは、また今度です!
Ken
こんにちは!みなさん、数直線をしっかり使いこなしていますか??
数直線は、正の数・負の数の単元で登場する数学の道具です。はじめて「数直線」という言葉を耳にした方のためにブリタニカ国際百科事典で調べてみると、
実数を表わす直線。1つの直線 l を考え,l 上に1点Oをとり,0と対応させて E0 とし,また長さの単位を定めて,E0 から単位の長さだけ進んだところを E1 とし,線分 E0E1 に数1を対応させる。
だそうです。ちょっとわかりにくいのでシンプルにしてあげると、
数字を表現できる直線(一部をのぞくよ)
というわけですね。1000も-90もなんだって1つの直線で表すことができるのです。よくよく考えてみると、数直線ってスゴいですね。
それでは数直線を使いこなしてみましょう!
数直線には以下のような3つのルールが存在しています。
数直線はかならず「直線」でないといけません。曲線を含んでいたり、
凹凸があってはいけません。
数直線にアクセントをつけたい気持ちはわかります。がしかし、ここはいたずら心をぐっと抑えて「直線」をひくようにしましょう。
つぎに、数直線のうちのどちらのサイドを「負の数側」、「正の数側」にするのかを決定します。さもなくば、それぞれがオリジナルの数直線を使いだします。
みんなちがって、みんないい
と詩人の金子みすずはかつていいましたが、数直線の場合は「みんな一緒」にしましょう。
ルールは簡単。原点(0)よりも左の直線側を「負の数(−)」とし、逆に右の直線側を「正の数(+)」とするだけです!!
それじゃあ、いったい全体、数直線という数学のアイテムを使って何がお得なのでしょうか?? お金がもらえる? モテる? お腹がいっぱいになる!?
いやいや。じつは冷静になってみると、以下の3つのメリットが数直線にはあることを気づかされます。
ひとつめの数直線のメリットは、
絶対値を理解しやすい
ということです。絶対値とは「絶対値の意味を5秒で理解できる方法」という記事でお伝えしたとおり、
ある数字の原点(ゼロ)からの距離
でしたね。一見、わかりにくい絶対値の概念です。だがしかし、数直線という数学のアイテムを駆使してやると、急にわかりやすくなっちゃうんです。
たとえば、-9の絶対値。「ねえねえ、-9の絶対値って何なのよ? 教えないとぶつわよ?」と美女に迫られても即答できません。これは肉体的な痛みを伴いますし、おおいにチャンスを逃しています。
そこで登場するのが「数直線」。直線を書いて、原点(ゼロ)をとって、ゼロより左側に9ついったところに「-9」をプロットします。
すると、この数直線を眺めているだけで「-9」の絶対値を察することができます。なぜなら、-9が0より9つ左に離れていることがわかるからです。
数直線を使えば「絶対値の意味」を視覚的に理解できるわけですね!あー便利便利!
ふたつめのメリットは「数の大小」です。2つの数字を数直線上にプロットする。これだけで2つの数の大小関係を3秒、い、いや、1秒ぐらいで理解することができます。
たとえば、「-0.5と-0.3のどちらが大きい数字ですか??」と問われたとしましょう。こんなときは、頭の中だけで考えるのでなく、実際に数直線上に2つの数字を書き出してみればいいのです。こんな感じで↓↓
すると、「-0.3」のほうが「-0.5」より右にあるため、「-0.3」のほうが大きい数である、ということがわかります。数の大小の問題がテストに出たときは迷わずに数直線上に書き出してみましょう。
最後は「正の数と負の数が混じった計算」を楽におこなうことができる点です。
+と−の符号が入り交じった計算は馴れるまでに時間がかかります。まず2つの数の絶対値の大小を比較して、こっちがでかいからあっちをひいて・・・などなど。これではひとつの数学の問題に時間をかけすぎてタイムアップになってしまいます。
そこで登場するのが、数直線というヒーローなのです。実際の例題で確認してみましょう。-9+2という計算問題があったとします。これを実際にといてみると、
という計算過程を踏まねばなりません。一見シンプルな計算にみえますが、思考の過程を書き出してみると複雑であることがわかります。
それでは、この計算に数直線を使ってやるとどうなるでしょうか??
まず-9を数直線上にプロットします。
これに2と足すということは、数直線上を右に2つすすむことを意味します。よって、-9にプロットされていた点は、
-7の点に移動します。つまり、この計算の答えは「-7」ということができます。
以上のように、数直線をつかえば「正の数と負の数の計算」を視覚的に、より直感的に理解できます。しかも、うっかり計算ミスをも防ぐ効果もあります。
テストで時間があまったときは数直線で答えを見直してみましょう!!
数直線が便利な3つの理由を紹介してみました。いかがだってでしょうか??
ぼくは中学生の頃、数直線を馬鹿にしていました。
こんなのただの直線だ! 子供だましだ!
なんて具合にです。 ただ、大人になってみて中学数学を復習してみて、
数直線は数字・計算を視覚的に理解できるツールである
ということがわかりました。数直線に惚れ直したというわけです。
これから中学の数学を勉強する読者の方は未来があります。せっかく中学校で「数直線」を学習しますので、積極的に利用してみてくださいね!
それでは、また今度です。
Ken
こんにちは、この記事をかいているKenです。今日も一緒に中学数学の勉強をはじめましょう!
中学数学の「正の数・負の数」という最初の単元。
ここで一番存在感をかもしだしているのは、
絶対値(absolute value)
という数学用語です。
絶対値なんて小学校の算数では登場しなかったし、日常生活で使われることはありません。
決して、「おまえの絶対値すごいよなああ」なんて会話はしませんよね?
そこで、今日は、絶対値の意味をわかりやすく解説してみました。
絶対値の意味にピンときてないときは参考にしてみてください。
それでは、中学の数学で登場する「絶対値」の意味を確認してみましょう。
中学校の教科書には次のように「絶対値の意味」が解説されています。
数直線上で、0からある数までの距離を、その数の絶対値といいます
この絶対値の意味の説明文を読んだだけではおそらく、
「え?数直線?」
となってしまうでしょう。
たしかに堅苦しい説明ですし、わかりづらいし、おもしろくないですよね??
はっきり言って、絶対値の意味の本質をとらえきれていません。
それでは絶対値の意味とは何なのでしょうか?!?
ズバリわかりやすく言ってしまうと、
「ある点」からの距離
です。
これこそ絶対値の本質的な意味なのです。理解を深めるために次のケースを考えてみましょう。
体育祭・運動会では徒競走がおこなわれますよね??
このタイプの徒競走ならば、
誰が勝者なのかわかりやすい
という利点があります。
同じ方向に同じスタート地点からゴールを目指して走るからわかりやすいのですね。
がしかし、しかしです。
砂漠のど真ん中に、校庭を持っている学校での徒競走はどうなるのでしょうか??
真っ白なラインをひけないし、第一、ゴールテープ持ち係があつくて立っていられないので、
10秒間でもっとも長い距離を走ったものを勝者とする
という徒競走のルールを定めました。
ここでいう「距離」とはスタート地点からの終了地点までの直線距離をあらわします。
図で表すとこんな感じになります。
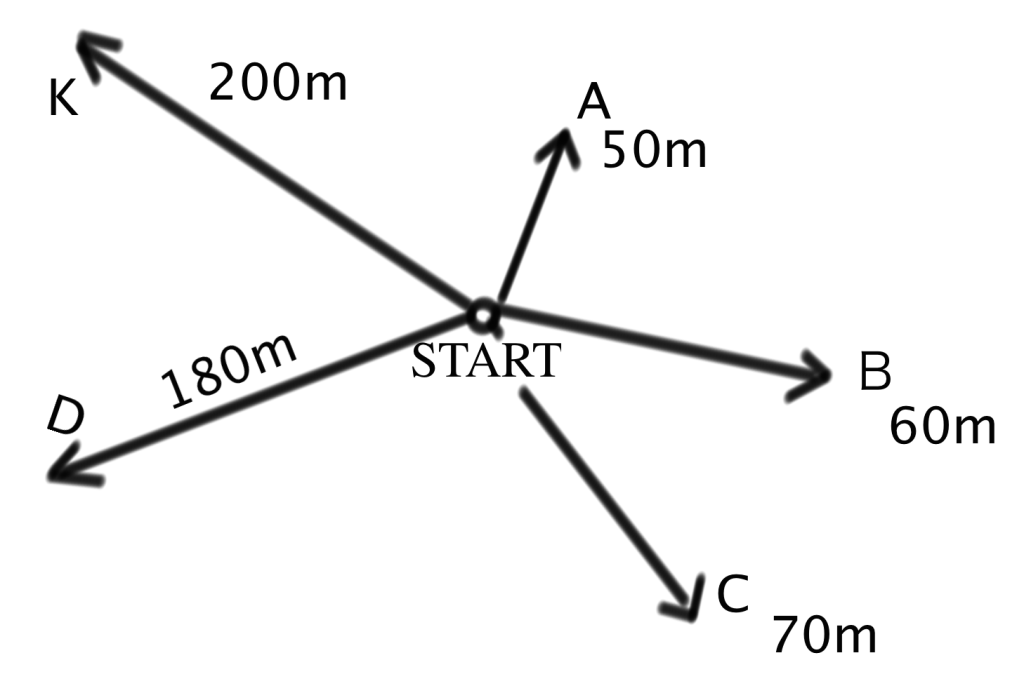
この砂漠徒競走の最大のポイントは、
徒競走の勝敗に「走る方向」がまったく関係しない
ということです。
つまり、右に走っても左に走ってもいいのです。
勝敗に関係あるのは「スタート地点からどれだけ走ったか」ということだけ。
それ以外の「走る方向」だとか、「履いてる靴の重さ」とかまったく関係がありません。
上の例でいえば、スタート地点から200mを走り抜いたK君が勝者というわけですね。
この砂漠徒競走における、
スタート地点からの距離(方向は関係ない)
が絶対値のことなのです。
以上の砂漠の話をまとめると、
絶対値とはある点からの距離を表しています。
しかもこれは「ある点」からどの方向への距離か、ということは一切関係ありません。
右だって下だって構いません。
これを数学の絶対値に置き換え直すと、「ある点」とは0のことになります。
したがって、数学の絶対値とは、
0からの距離(+だろうが−だろうが関係ない!)
のことなのです。
-9の絶対値は0から9離れているので絶対値は9。
同様に、15の絶対値は15、-200の絶対値は200というわけですね。

次回は中学数学に登場する「絶対値の問題の解き方」を解説していきます。
それでは、また今度です。
Ken
こんにちは!この記事を書いているKenです。久しぶりに天気が晴れて僕の心も晴れています。
中学数学で最初にぶつかる壁。
それは「負の数」という新しい数学用語です。小学校で学習していた算数には決して登場してこなかった数字の種類。
正の数? 負の数?? なんじゃそりゃ?
こんな感じで新しい数学用語に困った顔を浮かべている方もいることでしょう!!
しかしながら、です。
「負の数」は身近な例でたとえると分かりやすくなります。
数学の教科書でイヤイヤ勉強していては、「負の数」を上手に理解できません。中学校の数学の教科書はかなりお固く、具体例に乏しいですからね。中学校で勉強しはじめた数学を嫌いになってしまいそうです。
そこで、今日は思い切って「負の数」に関する記事を書いてみました。「負の数」を100%、イヤ、2000%ぐらい理解できる3つのストーリーを紹介します。
「正の数・負の数」の単元で泣きそうになっている方!よかったら参考にしてみてくださいね。
負の数とはいったい何者なのでしょうか?!? 数学の教科書にはこのように記載されています。
0より小さい数を負の数といいます。
うん、ものすごく分かりやすい「負の数」の意味ですね。ゼロよりも小さい数字を表現するために「負の数」、つまりマイナスという概念が生まれたのです。ふむふむ・・・・・
だけれどもだけれども!
なんだかしっくりこない。なんだ? 「ゼロより小さい」数だって?? わ、。わせるな!
ぜったいにそんな負の数なんて指じゃ数えられないし、目にも見えません。これじゃあ、中学数学で初めて「負の数」を目撃した中学生たちは困惑するはずです。そんなんじゃ、のちの中学校生活の将来が危ぶまれます。残りの3年間、数学嫌いで終わってしまうのでしょうか??
そんな事態を防ぐため、今日は、
なぜ「負の数」という概念が必要になったのか??
そんな原点を振り返ることにしましょう。
むかしむかし、あるところにセルシウスという男がいました。1700年代の半ばの話です。彼は、
水が「沸騰して水蒸気になる温度」と「氷になりはじめる温度」を100等分することで、温度をはかる指標を創りだしました。
その新しい温度の指標とは、「セルシウス(℃)」という温度の単位です。ぼくらの日常生活で頻繁に利用されています。たとえば、美しい天気おねえさんが、
今日の気温は39℃となるでしょう。超真夏日ですね!
と叫んだとしましょう。これが意味することはただ暑いということはもちろんのこと、
水が気体になるための温度の40%ぐらいの暑さなんだなあ
ということがわかります。 温度の単位のセルシウス℃の意味をたどればそんなことが分かってしまうのです。
がしかしながら、です。
日本の西部や関東圏ではなく、北海道の温度をはかろうとすると問題が生じます。なぜなら、
北海道の冬の温度は、0℃(水が氷になりはじめる温度)よりも低いから
です。これはセルシウスも予想外のことだったでしょう。0よりも低い温度を表現しなければ、北海道の本当の寒さを理解することができません。青森県と北海道の寒さの違いを教えて? なんて美女に迫られても即答することはできません。多いにチャンスを逃しています。
そんな由々しき事態に登場するのが「負の数(マイナス)」という数学の概念なのです。0よりも小さい数字。これがあることにより、
北海道と青森県の寒さの違い
を数値で表現することができます。たとえば、負の数、つまりマイナスの表現を使ってやれば、
1月の北海道の最低気温 -7.0℃
1月の青森県の最低気温 -3.9℃
と両者の気温を数値で表現することができます(気温と雨量の関係より)。さらに二つの温度差をも計算することができるので、
-7.0-(-3.9) = -3.1
つまり、二つの都道府県の1月の最低気温の差は「3.1℃」ということになります。
こんな感じで「負の数」という新しい数学の概念が活躍するわけですね!!
2つ目のお話は「借金」です。
毎月500円のお小遣いをもらっている小学生がいたとしましょう。彼は毎月、定価500円のコロコロコミックを買うことを生き甲斐にしています。来月は好きなマンガがどんな展開になるのか? どんな新しいキャラクターが登場するのか。そんなことを励みにしながら辛抱強く小学校に通っています。
がしかし、です。
ある日、どうしても手にいれたいオモチャが発売されました。それは単なるベーゴマでしたが、手作りをすることは不可能。クラスの友達がみんな持っているし、買わないと仲間はずれにされる。
あろうことか、そのオモチャの定価は1000円。これではコロコロコミックの購入を2ヶ月は控えないといけないことになります。せっかくの楽しい小学校生活が水の泡に。もうお先真っ暗です。
そんなときに登場するのが「負の数」という数学の概念なのです。負の数をつかえば「人にお金を借りること」、つまり「借金」を数字で表現することができます。
先ほどの例でいえば、ベーゴマを買うために1000円の借金を親御さんにしてみる。そうすると、この小学生の財布の中身には、
1000円札
が入ります。しかし、1000円のベーゴマを買ってしまうと財布の中身は0になります。しかもしかも、ほんとうに少年がもっているお金は-1000円ということになります。なぜなら、1000円という前借りしたおこづかいを両親に返済しなければならないからです。
したがって、
この先2ヶ月、コロコロコミックを我慢して、1000円を貯金しないと少年の財布は0円に戻らず、負(マイナス)のお金が入った状態になってしまいます。 これはキツいですね。
まとめると、
人にお金を借りた状態をも「負の数」を使えば表現できる!
ということになります。
最後は恋のお話です。
ある日、好きな人ができたとしましょう。惚れた理由は「一目惚れ」。外見と雰囲気だけで人を好きになってしまいました。彼女をなんとかガールフレンドにしたい。そんな息苦しさを感じたとしましょう。
この彼女と何も接触を持たない状態
が0、です。彼女は自分のことは何も知らないのです。このまま現状を維持していてはいつまで経ってもガールフレンドにすることはできません。
つぎに、彼女に何らかのアプローチをした状態を表せるのが、
正の数
という表現。彼女に勇気を持って話しかけてみる。プレゼントをしてみる。傘を貸してみる、など様々なアプローチをしてみたとしましょう。
彼女のためをおもってした行動は、正の数、つまりプラスの出来事として彼女の脳内に蓄積されています。正の数のイベントを増やしていけばいくほどガールフレンドをものにできる可能性が高まるというわけです。
がしかし、しかしです。
もし、もしも、彼女がいやがる行動をとってしまったらどうなるでしょう?!
そうです。自分に対する評価が下がってしまうのです。お茶を彼女の服にこぼした? 彼女に借金をした?? 話がつまらない?? ギャグがすべった???
そんな彼女の評価を下げる行動の「度合い」を表現することができるのが、
負の数
という数学の概念なのです。
先ほどの例をつかってみましょう。もともと彼女の評価ポイントが6あったとします。正の数です。
そこへ、
お茶をこぼした(-3)
借金をする(-4)
話がつまらない(-7)
ギャグがすべる(-90)
というイベントを積み重ねると、
彼女の評価ポイント= -98
という大きな「負の数」になってしまいます。これでは彼女に好かれるどころか嫌われてしまう、という事態に陥ってしまいます。これじゃあいつまで経ってもガールフレンドをゲットすることができません。
そんなモテナイ男の状態を数字で表現することができるのも「負の数」の魅力ですね。
負の数を理解するための3つのストーリーはいかがだったでしょうか!??
なんだか少々話がずれってしまったような気がしますね。
中学数学で一番はじめに勉強する「正の数・負の数」で挫折しそう・・・・・
なんて悩みを抱えている方がこの記事を読んで、
ああーなんだ!負の数チョー身近じゃないか!hahah
という幸せな気分になってくれたら嬉しいです。
これから中学数学を根気づよく一緒に勉強していきましょう!
それでは、また今度です。
Ken
中学数学で勉強する内容を知りたい。
そう思うときありますよね?? とくに、中学校にこれから入学する小学生の方。どんなむずかしい数学の単元が用意されているのか気になってしょうがないですよね。

がしかし、です。
中学校3年間で勉強する数学の単元の数はぜんぶでなんと21単元もあります。ときがすぎて21世紀となりましたが、中学で勉強する数学の単元が21個もあるなんてげせませんね。
誰でもいいから端的にシンプルに中学の数学の内容を教えてほしい。そう思いませんか??
じつは。じつは、です。
中学3年間で勉強する数学の内容はおおきくわけて4種類しか存在しないことがわかりました。4種類ですよ?? ワン、トぅー、スリー、フォーです。フォー。
の4つです。今日はこれらの中学数学の単元をわかりやすく紹介していきます。広い視野をもって中学の数学を勉強していけばきっと、言われるがままに勉強するより吸収がはやいはずです。中学校の数学で挫折しないためにも、一から確認していきましょう!
ここでは文字通り「数学の基礎」を学習していきます。
中学校で勉強する数学自体が「数学」という大きな学問のほんの基礎的な部分です。がしかし、その「数学の基礎」を勉強するための基礎をまずは修得せねばなりません。
これはいったら、中学数学という大きなモンスターを倒すための装備、のようなものです。期末テストのような中ボス、高校受験のようなラスボスを倒すためには装備をせねばなりません。剣をかったり、盾をかったり、ビームソードを買ったりなどなど。
そんなのちのち勉強した効果がきいてくるのがこの「数学の基礎」というわけですね。ふむふむ。
具体的に勉強する数学の基礎の内容は以下の2つです。
この2つは数学を勉強する中で嫌というほど登場します。はい。もう嫌になるくらいです。でも逆にいったら、この2つさえ押さえておけば中学数学の攻略に近づくというわけです。基礎を甘く見ずにしっかり勉強しておきましょう。
2つ目に勉強することは「代数学(algebra)」です。これは小学校の算数では登場しなかった分野です。超シンプルにいってしまえば、
リアルの数字を英文字で表現してあれこれする分野
ということができます。数字ではなく文字で数式を表現することによって、より多くの事象を一般化することができます。
たとえば、「彼女できる曲線」なるものがあったと仮定しましょう。 xを彼女を口説いた時間、aを外見定数、bを財布の中身とすると、
y=ax+b
と表現することができるのです。このことからわかるのは、彼女と会話する時間がながければ長いほど、また、外見がイケメンであればあるほどガールフレンドを獲得しやすいことを表現できているわけですね。あ、あと財布の中身が重要ですね。
こんな感じで、現実社会で起きている事象を数式で一般化してものごとをとらえる学問が「代数学」です。中学3年間で勉強する数学の内容にふくまれる「代数学」の単元は以下の3つです。
もちろん、これら一つ一つの単元にさまざまな種類があります。たとえば、方程式だったら二次方程式とか連立方程式とか、です。また関数だったら一次関数、比例、反比例、二次関数、と行った具合で勉強していきます。
中学数学の特徴は、おなじ数学ジャンルをいっきに勉強しない点です。中学一年生のときには代数学をひたすら勉強し、2年生のときは幾何学を・・・なんていう分け方はしません。中学3年間をかけてじわじわと学習していきますので、心の準備をしておいてくださいね。
3つ目に登場する数学の内容は「幾何学(geometry)」です。これは三角形とか四角形とか三角柱などの図形について勉強していく学問です。
2つの図形の関係性を調べたり、図形の角度を推測したりするジャンルです。中学で勉強する幾何学で登場することがらは以下の2つしかありません。
定義とはものごとの意味のことです。たとえば、「三角柱とは三角形を底面とした空間図形である」、といった具合です。定義は超お偉いさんしか決められないので不動のものです。
一方、定理とは「定義をもとに導かれたことがら」のことです。たとえば、「二等辺三角形の底角は等しい」などです。ここで覚えておいてほしいことは、
すべての定理には理由がある
ということです。定義ではなく定理が登場したら、まずは定理がいえる理由をさぐる癖をつけましょう!
幾何学をしっかり勉強しておけば、かなり日常生活で役に立ちます。たとえば、大きなピザを彼女と切り分けるとき。8人でお好み焼き屋に乗り込んだ時に瞬時に一人当たりの面積を計算する能力。これらはすべて中学で勉強する幾何学で修得することができます。
最後に中学校で勉強する内容は「統計学(statistics)」です。
この数学のジャンルは非常にぼくらの生活に密着したものになっています。天気予報、テレビの視聴率などがその良い例です。この2つがやっていることは、
数多くのデータから規則性や傾向を見いだす
ということだけです。それ以上でも以下でもありません。ぼくらが町中で記入するようなアンケートだってその一種です。アンケートではぼくらの不規則で奇抜な行動や思いをデータにして傾向を見いだそうとしているわけです。
そんな超身近な「統計学」が中学の数学で登場する単元は以下の3つです。
です。なぜだか知りませんが、この統計学というジャンルは教科書の最後にかならず登場します。代数学や幾何学と比較すると、まるで影のような存在です。正直、中学校で勉強したことがあまり印象に残らないかもしれません。ぼくもつい最近までこいつの存在を忘れていたほどです。
こんな影のような数学の分野ですが忘れずに勉強してあげてくださいね。
以上でとりあげた4つの数学のジャンルだけ。これだけでいいんです。これだけが中学数学の内容なのです。
中学の数学で新しい単元を勉強するときは必ず、
いま自分はどの数学ジャンルについて勉強しているのか、
ということを意識してみてください。学校の先生は結構不親切なのでぶっちゃけ教えてくれません。えっ。それでは誰に質問したらいいのかですって!??
そ、そんなときはこの中学学生のための勉強サイトを覗いてみてください。
この勉強サイトには、
という記事たちが用意されています。
いま勉強している単元の正体が不明すぎて泣きそう・・・
そんなときこそ踏ん張り時です。これらの記事を読めばきっとしっくりぱっくりとするはずです。
それでは、また今度です。
Ken
中学生活もあと一年。中学3年生になると進路のことだとか、恋のことだとか、体育祭のことだとか気になりだす頃です。中学生活の中でもっとも忙しく、もっとも思い出に残る一年なんかじゃないですかね!

・・・・・・ところが、ですよ。ところが!
数学、という魔の学問だって忘れちゃいけません。とくに中学三年生なってから勉強する数学は1年生、2年生のころと比べてかなりパワーアップしています。
し、しかも迫りくる高校受験ではかなりの頻度で出題されます。こんな状況で、もし、もしですよ?? 中学3年生のときに数学の学習に手を抜いていたらどうなってしまうでしょう!? 想像するだけできつそうですね。
そこで、今日は、
中学校3年生のときに勉強する数学の単元8つをきれいに華麗にまとめてみました。
これから中学3年生になる中学生の方や、テスト前に中学三年生で勉強した数学の単元を復習したい方。そんな方々の参考になれば嬉しいです。教科書に掲載されている中3数学の単元は以下の8つです。
8つも数学の単元があって正直目がくらみそうです。ただ、がんばって諦めずに8つの単元を数学のジャンル別に分類してみました。す、すると、
の4つの数学ジャンルにわけることができたのです。今回は中学3年生の数学単元をわかりやすく4つの種類ごとに紹介していきます。
それでは上から順番に見ていきましょう!
1つ目に勉強する単元は「数学の基礎」です。中3の数学単元で学習する内容の一つに「数学の基礎を勉強するための基礎」なる単元が登場します。
それは、
平方根(square root)
です。平方根とは簡単にいってしまえば、
二乗すると「ある数」になる数
です。なんだかむちゃくちゃ分かりづらいですね。 たとえば、√2 でしたら、√2を二乗してやると「2」になるわけです。つまり、二乗すると√記号の中身の数字に変化する、というわけですね!
えっ。なぜ平方根という基礎を中学三年生で学習するのかですって!?
それはのちのち勉強する「二次方程式」という単元で必要になるからです。平方根の知識がないと二次方程式をどう汗をかいても解くことはできないのです。
まずはこの数学の基本となる概念を押さえておきましょう。
2つ目に勉強していくのが「代数学(algebra)」というジャンル。中2数学単元の記事などで説明しましたが、
数字を文字でおきかえて考え事をする
という数学の学問です。 リアルの数字を文字(aとかb)で置き換えることによって、求めたい値を抽出したり、身近なことがらを一般化したりできます。
たとえば、ぼくの財布の中身を代数学を用いて表現してみましょう。ひと月の稼ぎは7万円しかないです。デートに行く回数をひと月あたりx回とします。一度のデートには6000円かかるので、
70000 – 6000x
という文字式がぼくの財布の中身を表しています。 つまり、財布の中身を文字で一般化してやることで、デートの回数に応じた財布の中の残金がわかるというわけですね。ふむふむ、すこし興味深い。
中学三年生で登場する「代数学」の単元は以下の3つです。
中学三年生の数学でまず初めに勉強するのがこの単元。ここで勉強する内容は以下の2つです。
ほら? とてもシンプルですよね。αの行為を数学では「展開 (expand)」といい、βの行為を「因数分解(factorization)」と呼んでいます。この2つが中学3年生で学習する数学の基礎の部分です。ここを理解しておかないと中盤に登場する「二次方程式」でつまづくことになってしまいますよ!
おつぎに登場するのが「二次方程式(quadratic equition)」という数学の単元です。これは文字通り、
次数が2である方程式
のことです。中学1年、2年で勉強してきた数学では「次数が1次」の場合のみでした。二次方程式とはたとえば、
式
のような感じです。かなりごっつくて腕力がありそうな数式ですね。
だがしかし、です。
これまでに勉強した「平方根」と「因数分解」をしっかりマスターしていればなんのこっちゃありません。方法さえ覚えてしまえばカップラーメンより簡単です。あ、おいしいかは不明ですけど。
ただ、以上の2つの単元をまだ完全に修得していない方にとってはかなりキツいかもしれません!勇気を持って復習してみましょう。
3つ目に代数学の分野で勉強するのは「二次関数(quadratic function)」です。これも二次方程式のときと同様、非常にシンプル。つまり、
次数が2次の関数の勉強
というわけです。中学3年生になるまで比例、一次関数と学んできました。中学数学の集大成の三年生では、次数を二次まで増やした、
式
のような関数に挑戦するというわけですね。むずかしいように聞こえますが、勉強する内容はこれまでと一緒です。
です。この2つができれば中学で学習する関数なんてイチコロです!
幾何学(geometry)とは超シンプルにいってしまえば、
図形のお勉強
です。三角形とか四角形をこれでもか!というほどいじくりまわす数学のジャンルです。中学3年生のときに勉強する幾何学は以下の3つの単元となっています。
「掃除(そうじ)」ではなく「相似(そうじ)」をここでは勉強します・・・・
中学の数学の先生がこんなギャグですべっていたのを今でも思い出せます。
そう、ここで勉強するのは幾何学の一つのジャンルである「相似(similarity)」です。相似とはいわば拡大と縮小の関係のこと。たとえば、下の正方形くんと、
その子供の正方形ちゃんは、
相似の関係にある、と言うことができます。なぜなら、両者は拡大・縮小の関係にあるからです。大きくすれば一緒。小さくすれば一致する。そんな図形同士の複雑な関係について勉強していきます。
2つの相似な図形はどの程度の比率になっているのか?? また、どんな条件をみたす図形同士が「相似」ということができるのか!?
そんなことに注目しながら勉強をすすめてみてくださいね。
おつぎは「円(circle)」についてみっちり学習する数学の単元です。ただ、円の勉強といってもここで触れる内容はただ一つです。それは、
円と角度の関係
です。こいつを押さえてしまえばこの単元はクリアしたも同然です。円周上の角(円周角)や中心と円周上の2点がおりなす角(中心角)の関係。これに関する性質がじゃんじゃん登場します。円の公式をまる暗記することも大切ですが、忘れないでほしいのは、
なぜその性質がいえるのか
を検証することです。数学の教科書で語られているすべての「性質」には理由があります。なぜ? なぜ?? なぜ???という問いかけを忘れずに読み進めていってほしいですね。
高校受験でかなりの頻度で登場するのがこの「三平方の定理」という単元。
発見者のオッサンの名前にあわせて「ピタゴラスの定理(Pythegorean theorem)」なんて呼ばれたりします。これは直角三角形の3つの辺の関係をあらわした超重要かつシンプルな定理です。たとえば下のような直角三角形の形をしたピザがあったとしましょう。
そしたら、この美味しそうなピザの3つの辺の長さの関係は、
c^2 = a^2 + b^2
となります。これがピタゴラスという男が古代エジプトで発見した直角三角形の定理なのです。こいつを日本ではなぜか「三平方の定理」と呼んでいます。この定理をもちいて、あんなことをしたり、こんなまねをしてみたりするのですね。なるほど。
最後に「統計学(statistics)」の勉強を中学3年時にします。統計学とは、
たくさんの不規則なデータを集めて、ある規則を見いだす学問
のことです。中学1年、2年生では「確率」や「度数分布」などを勉強してきましたね。中学3年生でもちょこっとだけ統計学の分野を勉強していきます。
中学数学の教科書の単元でいえば、
標本調査(Sampling)
という単元です。ここでは、世の中の統計学にもとづいて行われた調査がどのような仕組みで行われるのか、といったことを勉強していきます。
たとえば、テレビ番組の視聴率。テレビは無料でみれますよね? あっ、NHKとか衛星放送をのぞく民放の話ですけど。なぜ民放が無料で視聴できるのかというと、
広告主が広告をだしてお金を払っているから
ですよね。そこでこの「広告主」はなるべく多くの人に自社の広告をみてほしいわけです。
そこで登場するのが「テレビ視聴率」という標本調査。
テレビ局はなるべく全国民のテレビに視聴率調査機をとりつけたいですが、手間と時間と金がかかる。そこである一定数のテレビ視聴者(標本)に協力してもらい、データをとることにしました。
ここでいう「全国民のテレビ視聴状況を確認すること」を「全数調査 (census)」といい、「ある一定数の視聴者をぬきだして調査すること」を「標本調査(sampling)」と呼ぶわけです。
そんなこんなで、標本調査はとても身近で役に立つお勉強です。受験勉強で忙しい時期かもしれませんが、こっそりと勉強しておきましょう!
ふう。ここまで8つの数学単元を4つの種類に分類してきました。ここでは最後にもう一度整理して、それぞれの単元ごとの関係性を図で確認しましょう!
この図からもわかる通り、中学三年生の数学は中学1年、2年で学習した内容をもとにレベルアップしてきたものです。
中学1・2年で勉強してきた内容を理解していないと、中学3年生の数学で遅れをとってしまうことになります。決して、中学3年生の数学からまじめに勉強しようとしても借金は帳消しになりませんからね!。
ただ、誰でも数学の基礎さえしっかり理解できれいれば中学三年生の数学だって攻略できます。これから一緒にゆっくり勉強していきましょう。
それでは、また今度です!
Ken
これから期末テストだから中学二年生の数学の単元を振り返りたい。
せめてどんな数学の問題が出題されるか知っておきたい。
そんな中学数学の悩みを抱えていませんか!?? 期末テスト3日前とかだったらヤバいですが、1ヶ月前とか二週間前とかだったらどうにかなります。これからみっちりと勉強すればですけどね。

さっそく、大急ぎで中2の数学の単元を振り返っていきましょう! 中学二年生で学習する数学の単元は以下の6つです。
なんだろ・・・・6つ!? 6つとかありすぎて数えられないし覚えられない!しかもやる気もでませんよね!? これじゃあいつまでたっても期末テストの勉強なんてできる気がしません。
あっ。ああ! 6つの数学の単元もジャンルごとに分類すると、3つになるじゃありませんか! 3つですよ?3つ!これは記憶力がとぼしいぼくでも覚えられそうです。
そこで今日は以上の6つの中2数学の単元を、
の3つにわけて紹介していきます。3つにわければなんとか覚えられそうですね。
まず一つ目に中学2年生のときに学習する単元は「代数学(algebra)」です。代数学とは超むずかしいように聞こえてしまいますが、内容はいたってシンプル。代数学をものすごく簡単に表現してしまうと、
数字を文字で代用してアレコレする学問
のことです。中学1年生で勉強した方程式や比例・反比例の関数がこれに相当しますね。中学二年生では一年生の内容がちょっとだけ難しくなっています。以下の3つの代数学を学習していきます。
中学1年生で勉強した「文字の式」という単元をちょっと進化させたものです。中学2年生で習う文字式の最大の特徴は、
ひとつの式で使う文字の数が増えた
ということです。中学1年生で勉強した文字式には、
2x+8 = 90
のように「x」という一つの文字しか登場しませんでした。がしかし、中学2年生の数学では、
a+2b+3c = 90
のようなaとかbとかcがじゃんじゃん登場してきます。
えっ。なぜ文字の種類が急激に増えたのかですって?!?
それは、のちのち勉強する「連立方程式」と「一次関数」で文字の種類がたくさん使われるからではないでしょうかね。えっ! こわいですって? 大丈夫大丈夫です。ただ単に文字が増えただけですから。
中学2年生になっても方程式を勉強せねばなりません。しかも、今回の方程式はなんと文字数が増えます!
えっ。あ、いや。「方程式」から「連立方程式」のように2文字だけ文字数が増加したのではありません。 連立方程式には、
2つ以上の文字(変数)
が登場します。たとえば、
x+y=900
2x-9y=12
などのような方程式。連立方程式では、
が使用されます。なんだかかなりレベルアップしているような気がしますね。 ただ、ちゃんと基本を押さえれば冷静にとくことができます。コツコツと一緒に勉強していきましょう!
最後に学習するのは「一次関数」。中学1年生のときに勉強した「比例」を少しだけ応用した関数の単元です。「一次関数」とは、
次数が一次の関数のこと
です。つまり、「次数とは何か?」ということと「関数とは何か?」ということを押さえておけば簡単にとくことができます。
この単元では関数をグラフにする能力と、関数の性質(傾きと切片)を解答する力が問われてきます。こんな感じですね↓↓
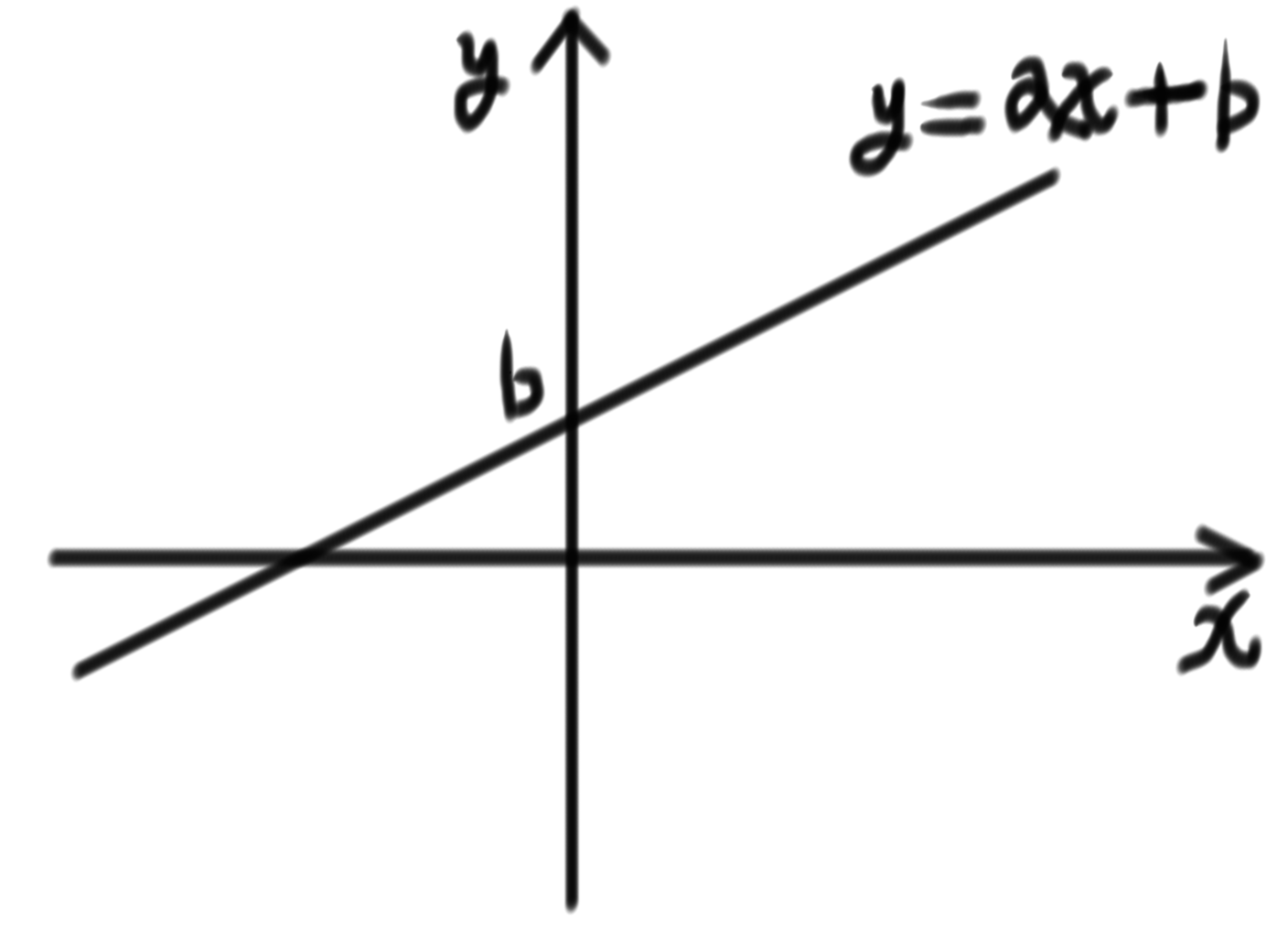
基本的な問題の解き方を押さえてしまえばあとは楽勝です! ゆっくり勉強していきましょう!
さて、お次に中2数学に登場するのが「幾何学(geometry)」というジャンルの数学。これはものすごく簡単にいってしまえば、
図形をいじり回す数学のジャンルの一つ
ということができます。
中学1年生では二次元の「平面図形」と三次元の「空間図形」の2種類の幾何学を勉強しました。なんとラッキーなことに、中学2年生では「平面図形」だけにしぼって学習していきます。具体的な単元は以下の2つですね。
この数学の単元では平面図形の基本的な事項をみっちり勉強していきます。
とくに以下の3つのことにフォーカスしています。
これらは次の「図形の性質と証明」という単元を理解するのに必須の内容たちです。これをちゃっちゃとクリアして次の単元に乗り込んじゃいましょう!
中学数学の山場のひとつである「図形の証明」がこの単元で登場します。もっとも中学数学で挫折する生徒が多い単元です。心してかかりましょう。
ここではちょっと特殊な「三角形」と「四角形」の性質を勉強していきます。しかも、単に図形の性質を暗記するのではありません。図形の性質を「証明」という方法を用いて明らかにしていくのです。
たとえば、
二等辺三角形の性質
です。
二等辺三角形とはどのような三角形を指しているのか。また、この三角形には他の三角形とは異なるどんな性質があるのか。そういう細かいことをじゃんじゃん証明していきます。図形好きにとっては堪らない数学の単元となることでしょう!
中学二年生のさいごに「統計学(statistics)」という数学ジャンルを勉強します。統計学とは超シンプルにいってしまえば、
たくさんのデータの中からある規則性や法則を見いだす学問
です。中学二年生ではその統計学のうちの「確率(probability)」という分野を勉強します。確率とは、
あるものごとが発生する度合い
のこと。たとえば、毎日確認している「天気予報」なんかが良いその一例です。明日はデートだけど、降水確率が90%!? そんな降水確率が意味しているのは、
10回デートしたら9回雨がふる可能性がある
ということです。雨が降らない可能性もありますが、これはずいぶん絶望的ですね。 つまり、降水確率は「雨がふる」可能性を度合いで表現してくれているわけですね。
ギャンブルやゲームが好きな中学生は「確率」が好きになるかもしれませんね。
以上で中学二年生時に勉強する数学の単元の紹介は終了です。
やはりこの記事を書いていて感じたのは、
中学2数学は中1数学の単元をステップアップさせたものだ
ということです。つまり、中学1年生の数学でちょっとあやふやな箇所があれば、中学2年生の数学でつまづいてしまうかもしれません。中学2年生になる前に1年前に勉強した数学の内容を復習しておきましょう!
図で中学2年生で学習する数学を表現すれば次のようになりますね。
それでは、また今度です!
Ken
中学校の数学をどのように勉強したらいいかわからない。
中学校の数学の授業が意味不明すぎてついていけない・・・
そんな悩みをお持ちではありませんか?? そんな悩みを解消するために塾に通ってみたり、進研ゼミに入会してみたりしてはいませんか。
ぼくは現在、25歳のいい大人になりました。10年前に勉強した数学の教科書を2日間をかけて復習してみました。やっぱり中学校を卒業してから10年たつと、色々忘れていました。いやあ、年をとるって怖いですね。

そんな中学校三年間の数学を48時間で復習してみた結果、
中学で学習する数学で大切なことは3つしかない
ということに気づいたのです。3つですよ? 3つ。片方の指で数えられちゃいます。中学の数学の単元には図形とか文字式とか方程式とか関数とか山のようにありますが、どれも以下の3つを軸に解説されているのです。
どんなに複雑なことを説明している数学の教科書でも、ゼッタイに上のいずれかを解説しているのです。今日は、中学の数学を攻略するために必要なの3つことを徹底解説していきます。よかったら参考にしてくださいね。
中学数学の教科書で解説されている1つの事柄のうち、
定義(definition)
というものがあります。デジタル大辞泉によると、
物事の意味・内容を他と区別できるように、言葉で明確に限定すること。
とあります。つまり簡単にいってしまえば、
あるものごとの意味・内容
のことですね。たとえば、りんごを例にとりましょう。

「りんご」という言葉を耳にすると、以上のようなリンゴの写真を思い浮かべる方が多いのではないでしょうか??青森県に住んでいなくても、りんごの写真とかイメージを思い浮かべることができます。
しかし、「りんご」をまだ見た事がない人のために言葉で説明してほしい、と言われたらどうでしょう?? 今までそのような経験がありません。ぼくだったら苦し紛れに「えっと・・赤くて丸い甘い味のする果物・・・か、かな?」と説明するかもしれません。
この程度の説明では「りんご」を示しているのか、はたまた「熟したプラム」を説明しているのか検討もつきません。これではコミュニケーションを上手にとれていないことになります。
そこで登場するのが定義。りんごの定義(ものごとの意味)を確認してみましょう。デジタル大泉林によると、
バラ科の落葉高木。また、その果実。
とあります。植物をろくに勉強していないぼくにとって、正直、この定義はチンプンカンプンです。 だがしかし、このりんごの意味の説明は、「りんご」だけをピンポイントに説明しています。ゼッタイに「熟したプラム」の説明と混同することはありません。これが定義の性質の一つである
言葉で明確に限定すること
の意味です。
それでは、中学数学の教科書に登場する「定義(ものごとの意味)」にはどのようなものがあるでしょうか?!?
りんごの定義ほどエキサイティングではありませんが、とりあえず確認してみましょう。
たとえば、中学2年生の数学の単元で学習する「対頂角 (Vertical Angle)」を例にとりましょう。
対頂角の意味(定義)は、TOMACの数学用語集によると、
2つの直線が交わったとき出来る4つの角のうち、向かい合った角
だそうです。図で表現すると以下のようになります。
上の図でいえば、4つの角aとd、bとcがそれぞれ「対頂角」とよばれるわけですね。ふむ、かなり分かりやすい明確な定義です。定義の最大の特徴は、
定義には理由がない
ということです。なぜリンゴはリンゴなのか?? なぜ対頂角は対頂角とよばれるのか??
このような問いに答えはありません。強いて言うなら、
昔のお偉いさん方が勝手に決めたから
と答えるしかありません。それぐらい、数学用語もしかり、果物もしかり、定義にはゼッタイ的な権威があるのです。ごく少数の人間しか「定義」をいじることができません。
2つ目に中学校の数学で大切なことは「定理(theorem)」を押さえることです。定理とはデジタル大辞泉によると、
ある理論体系において、その公理や定義をもとにして証明された命題で、それ以降の推論の前提となるもの。
だそうです。ちょっと難しいので噛み砕いてみると、
定義(ものごとの意味)をもとにして証明されたこと
といえます。定義をもとにした事柄が定理というわけですね。中学校の数学教科書では「性質」と呼ばれていることが多いです。定義がなければ定理がない。定理がなければ問題が解けない。いわば、数学の問題をとくための道具(アイテム)のようなものです。
いまいちのピンと来ないです。先ほどの対頂角の例をもとに、定理を確認してみましょう!
対頂角の定義は、
2つの直線が交わったとき出来る4つの角のうち、向かい合った角
でしたね。この定義から導くことができる定理は以下のものがあります。
対頂角は等しい
というものです。下の図でいえば、
角A= 角D
角B=角C
というわけです。すべての定理には理由があります。なぜこの対頂角の定理がいえるのか。その定理が存在できる理由を探ってみましょう。
これは、
直線の角度は180度である
ということから証明できます。
角aとc上の直線がつくる角度は180度であるため、
角a+角c = 180度・・・・(1)
角cと角dに関しても同様のこと言えるため、
角c+角d = 180度・・・・(2)
(1)と(2)より、
角a = 角d
よって、対頂角は等しいといえるわけですね!
この対頂角の例のように、
定理には必ず理由があります。中学数学の教科書では「性質」という用語で教えられることが多いです。「定理」とか「性質」のようなワードが登場したら、その理由について考察する癖をつけておきましょう。
定理には存在する理由があります。よって、暗記しなくても全く問題ありません。必要最低限の公理や定義を頭にいれておけば、自分で導くことができるからです。
ただし、
数学の定理をおぼえておくと無茶苦茶便利である!
ということを忘れないでください。定理をおぼえていない中学生は、毎回、定理を定義や公理から導かなくてはなりません。いわば、数学の定理はRPGゲームでいえばアイテム。ソードや盾。ポケモンでいったらワザマシンの役目を果たしています。あってもなくても構わないが、ないと不便で攻略に時間がかかる。そういう性質を定理は持っているのです。
中学数学を攻略する最後のコツは「解法」を使いこなすことです。
解法とは、
数学の問題を効率よく解くための方法
のことです。方程式の解法を例にとってみましょう。方程式を解法するために知っておくべきことは、
等式の性質
だけです。これだけあれば、中学数学で登場する大抵の方程式をとくことができます。がしかし、これだけでは中間テストや期末テストで登場するモンスター級の方程式を倒すことはできません。せいぜい、相打ちが良いところです。
テストでよりいい点数をとりたい。速く休み時間でキャッチボールをしたい。
そんな中学生たちのために、方程式に関する解法がいくつか用意されているのです。
これらを知らなくても方程式は解けますが、知っていたら超便利。これが中学数学で登場する「解法」というやつらです。テストでいい点をとりたかったり、クラスの美女を振り向かせたい方は数学の「解法」を暗記することをおすすめします。
数学の解法は、ポケモンやドラクエに例えると裏技です。セレクトボタンを7回おしてポケモンセンターにポケモンを預ける。などといった、一気にポケモンのレベルを上げることができるチート手のたぐい。裏技を知らなくてもポケモンは楽しめますが、あったらもっと速く攻略できる。そんな感じです。
中学数学の各単元で学習する新しいことが、
定義なのか??
それとも、定理なのか??
それともそれとも、解法なのか???
ということを頭に入れておくとかなり吸収のスピードが異なります。数学というゲームを攻略する、という気持ちで中学数学を勉強していきましょう。この新しい用語はポケモンの名前なのか、ポケモンに技をおぼえさせるワザマシンなのか、それとも、一気にレベル100に到達するための裏技なのか。
そんな感じで、中学数学をこつこつと勉強していきましょうね。
それでは!
Ken