こんにちは!この記事をかいているKenだよ。水はペットボトルがいいね。
ひし形(菱形)の定義ってなんだろう??
だいたいの形はイメージできるんだけど、
「ひし形」の定義とか意味がわからないときもあると思う。
そこで今日は、
ひし形(菱形)の定義をわかりやすく解説していくよ。
よかったら参考にしてみてね。
〜もくじ〜
教科書によると「ひし形の定義」は、
4つの辺がすべて等しい四角形
だ。
ぜんぶの辺が等しい四角形。
ちょうどダイアモンドみたいなやつだね。
これが「ひし形」ってわけさ。
2つの辺がそれぞれ等しいだけだと「ひし形」にはなれない。
そいつは平行四辺形だ。
いや、角がぜーんぶ等しくってもダメだよ。
そいつは長方形になっちゃう。
角ではなくて、
4つの辺がすべて等しい四角形
を「ひし形(菱形)」とよんでいるんだ。
この定義をしっかりおぼえておこう!
ひし形の定義はわかったね??
でも、あと1つおさえておきたいことがある。
それは、
ひし形は平行四辺形の1種
ということさ。
つまり、
ひし形は平行四辺形である
といえるんだ。
えっ。
ひし形と平行四辺形を一緒にしないでほしいって???
いやいや。
これは事実、現実だ。
なぜなら、
4つの辺がすべて等しい
ってことは、
2組の辺がそれぞれ等しい
の平行四辺形になる条件をみたしているからね。
だから、ひし形である以上、
そいつは平行四辺形でもあるわけだ。
でもね、
平行四辺形はひし形とはいえないよ。
だって、
平行四辺形っていうだけじゃ4つの辺が等しくはないからね。
たとえるなら、
ひし形と平行四辺形の関係は「寿司」と「マグロ握り」の関係に似ている。
寿司屋にいくと、
うにだったり、
あなごだったり、
いくらとか食べられるよね。
そいつらをまるっとふくめて、
寿司
とぼくらは呼んでいる。
だから、マグロ握りというのは「寿司」というグループの一種にすぎないわけだ。
つまり、
マグロ握りは寿司である
といえる。
けど、その逆の、
寿司はマグロ握りである
とはいえないんだ。
ここでいう、
「寿司」が「平行四辺形」で、
「マグロ握り」が「ひし形」ってわけ。
つまり、
いろいろな平行四辺形の中の1種類として、
ひし形
があるってことさ。
この「平行四辺形とひし形の関係」はおさえておこう!
4つの辺がすべて等しい四角形
がひし形の定義だったね。
この定義から、
2組の辺がそれぞれ等しい
っていう平行四辺形になる条件が使えて、
ひし形は平行四辺形であることがいえるんだ。
テスト前にしっかり復習しておこう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。家系ラーメン、最高。
長方形の面積の求め方には公式があるよ。
ヨコの長さをa、タテの長さをbとすると面積は、
ab
で求められるんだ。
つまり、
(長方形の面積)=(タテの長さ)×(ヨコの長さ)
ってわけだね。
この公式ってむちゃくちゃ便利。
たとえば、ヨコ4cm、タテ3cmの長方形ABCDがあったとしよう。
この長方形の面積は、
4 × 3
= 12 [cm^2]
になるんだ。
公式でガンガン計算していこう!
でもさ。
なぜ長方形の面積が公式で求められるんだろう??
話がうますぎるね。
そこで今日は、
長方形の面積の求め方を3ステップで解説していくよ。
よかったら参考にしてみて。
「1cm×1cm」の正方形をイメージしよう。
この「ミニ正方形」が、
長方形に何個はいっているか??
を求めていくよ。
これはレンガの家の大きさを求めるときといっしょ。
この家の大きさを求めるときはどう計算する??
そう、
そうだよ。
1つのレンガ素材の大きさを求めて、
長方形にレンガが何個はいっているのか??
ということを考えていくはずなんだ。
同じことを長方形の面積でもやろうってわけさ!
「ミニ正方形」を長方形のヨコの分ならべてみよう。
たとえば、ヨコの長さが4cmの長方形だったら、
4つのミニ正方形がヨコに並ぶはず。
これで第2ステップ終了さ。
最後に、ヨコに増やした正方形たちをタテの分だけふやそう。
長方形のタテが3cmだとしたら、
4つのミニ正方形を3つずつタテに増やすんだ。
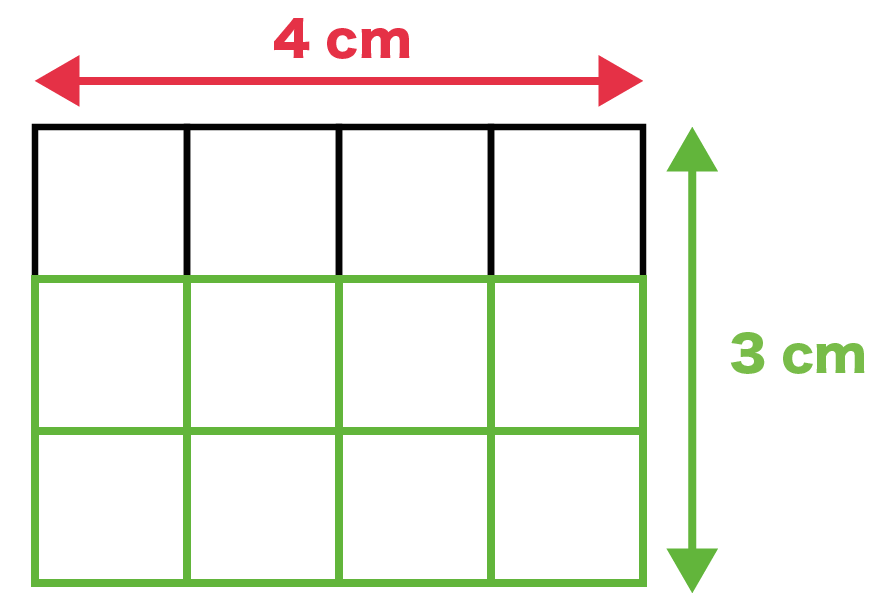
ミニ正方形の面積は1 cm^2だよね?
この長方形には12個のミニ正方形がひそんでいるから、
面積は、
12[cm^2]
になるんだ。
つまり、
「タテ×ヨコ」になっているわけさ!
長方形の面積の公式は、
タテ×ヨコ
で求めることができる。
公式で面積を計算していこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。ゴミ箱は2つほしいね。
長方形の定義ってなんだろう??
そう思うとき、
あるよね。
教科書によると長方形の定義は、
4つの角がすべて等しい四角形
らしい。
ぜーーんぶ角が等しいってことは、
1つの角はすべて90°ってことだね。
だって、四角形の内角の和は360°だからさ。
このタイプの四角形を数学業界では、
長方形
ってよんでいるんだ。
2つの角がそれぞれ等しくてもダメ。
そいつは長方形なんかじゃない。
すべての角が等しくても、五角形じゃダメ。
長方形とは呼べないね。
こんなやつらじゃなくて、
4つの角がすべて等しい四角形
が「長方形の定義」っておぼえておこう。
1つだけおさえておきたいことがある。
それは、
長方形は平行四辺形の1種
ってことさ。
つまり、
長方形は平行四辺形である
といえちゃうんだ。その逆はいえないけどね。
図でかくとこんな感じになる↓↓
世界中のいろいろな平行四辺形のなかの1つに、
「4つの角がすべて等しい四角形」という長方形がいるんだ。
この関係をたとえるなら、
炭酸飲料のなかのコーラみたいなもんさ。

世の中には、
コーラとか、
サイダーとか、
スカッシュとか、CCレモンとか、
たくさんの炭酸飲料が、いる。
その中のひとつに、コーラがあるよね??
この場合、
コーラは炭酸飲料である
っていえるけど、炭酸飲料はコーラであるとはいえないね。
炭酸飲料とコーラの関係でいうと、
「コーラ」が長方形っておぼえておこう。
でも、
なんで長方形は平行四辺形になるんだろう??
ちょっと不思議だね。
じつは平行四辺形になる条件の、
2組の向かいあう角はそれぞれ等しい
をつかっているんだ。
なぜなら、
4つのすべての角が等しいってことは、
向かいあう角同士も等しいからね。
つまり、
ぜんぶの角度が90°になって、
2組の角がそれぞれ等しいっていえるんだ。
だから、長方形は平行四辺形ともよべちゃうんだね!
長方形の定義はどうだった??
4つの角がすべて等しい四角形
が長方形だったね。
この定義も大事だけどそこから、
長方形は平行四辺形である
ってことも導けるようにしておこう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。水道水、うまいね。
四角形の内角の和
ってたまに求めたいよね??
そんなときは、
多角形の内角の和の公式をつかえば一発。
n角形の内角の和は、
180× (n-2)
で計算できちゃうんだ。
四角形の内角の和は、
nに「4」を代入してやればいい。
すると、
180× ( n -2 )
= 180 × (4-2 )
= 360°
って計算できちゃう!
つまり、四角形の内角の和は、
360°
になるんだ!!!
でもさ、
なぜ四角形の内角の和は360°になるんだろう??
便利すぎてこわいよね。。
せっかくだから、
内角の和が360°になる理由をさぐっていこう。
その理由はずばり、
四角形に「三角形が2つ」含まれているからなんだ。
対角線をすーーーっとひいてみよう。
すると、
そこには、
三角形が2つ出現しているはず。
んで、
三角形の内角の和は180°だったよね??
ってことは、
三角形が2つ隠れている四角形の内角の和は、
180°×2
= 360°
になるってわけ。
これで四角形の内角の和を計算できたね。
多角形の内角の和を求めたいときは、
三角形が何個かくれているのか??
を調べてみよう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。徒歩は5分だね。
台形の面積の求め方の公式っておぼえてる??
「上の辺」をa、「下の辺」をb、「高さ」をhとすると、
(a+b)×h ÷2
で計算できちゃうんだ。
つまり、
(上の辺+下の辺)×(高さ)÷2
でいいんだ。
たとえば、
の台形ABCDがあったとしよう。
このとき、台形の面積の公式をつかうと、
(上の辺+下の辺)×高さ÷2
= (4 + 8 ) × 6 ÷2
= 36 [cm^2]
になる。
くそ便利な公式だね!
でもさ、待ってよ。
台形の面積の公式は便利だけど、
なぜ公式がつかえちゃうんだろう??
「上の辺」と「下の辺」をたすだって??
まったく謎すぎる。。
そこで今日は、
台形の面積の求め方の公式をわかりやすく解説していくよ。
つぎの3ステップで計算できちゃうんだ。
例として、
の台形ABCDの面積を求めてみよう。
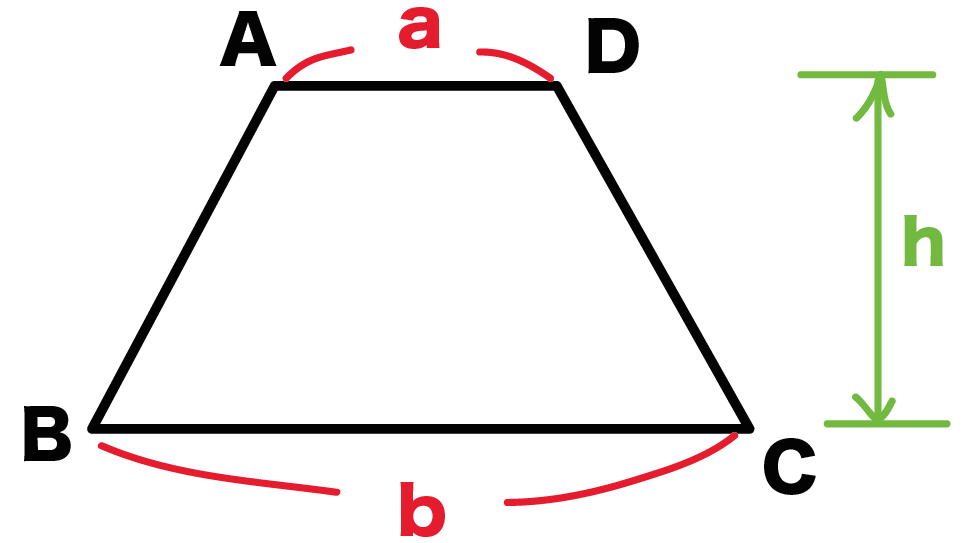
台形に対角線をひこう。
1本でいいよ。
台形ABCDでいうと、
BとDをむすんでみようか。
これで対角線BDのできあがりさ。
対角線をひくと、
台形が2つの三角形にわかれたね??
コイツらの面積を計算していくよ。
台形ABCDでは対角線BDをひいて、
の2つの三角形にわかれたね。。
△ABDは、
の三角形。
三角形の面積の公式をつかえば、
△ABDの面積は、
a × h ÷2
= 1/2 ah
になる。
おなじように、
△BCDの面積を計算しよう。
公式をつかうと、
b × h ÷2
= 1/2bh
になるね。
最後に、2つの三角形の面積をたそう。
たしてやると、台形の面積になるはず!
台形ABCDの場合、
をたそう。
すると、
△ABD + △BCD
= 1/2 ah + 1/2 bh
= 1/2h (a+b)
になるね。
これが台形ABCDの面積さ!
だから、
台形の面積 = 1/2h (a+b)
= (上の辺+下の辺)×高さ÷2
になるんだ。
これで、台形の面積の公式が導けたね !
台形の面積の公式は簡単。
(上の辺+下の辺)×高さ÷2
で計算できちゃうんだ。
おぼえることも大事だけど、
なぜ公式が使えるのか??
ってことも押さえておこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。洗顔大事だね。
三角形の面積の求め方の公式。
それは、
底辺×高さ÷2
だ。
底辺をa、高さをbとすると、
1/2ab
であらわせるってわけ。
たとえば、
底辺6cm、高さ4cmの三角形ABCがいたとしよう。
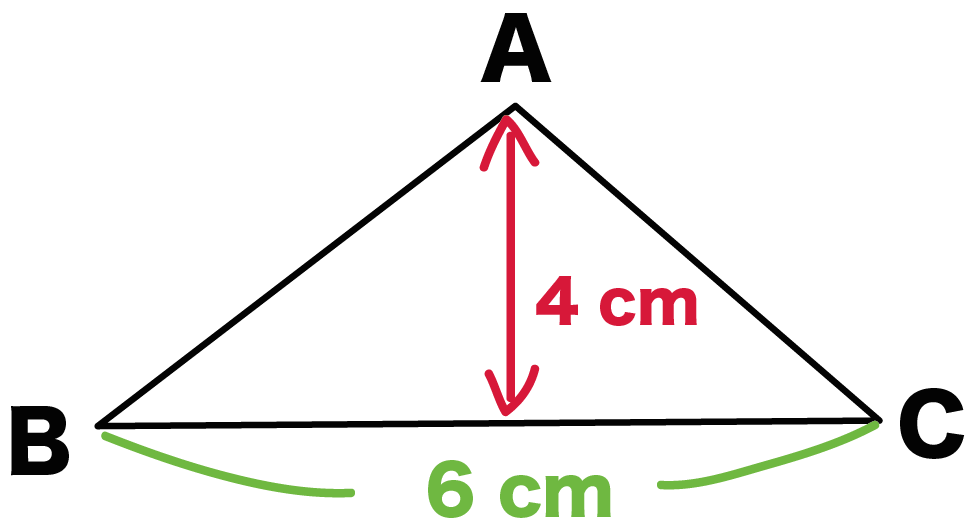
こいつの面積は、
6×4÷2
= 12 [cm^2]
になるよ。
「底辺」と「高さ」がわかれば計算できちゃう。
この公式すげえ。
でもさ、
なんで公式が使えるんだろう??
関係のない「底辺」と「高さ」をかけて、
2でわったらなぜ面積になるのか?
ちょっと白黒つけたいよね。
そこで今日は、
三角形の面積の求め方を3ステップで解説していくよ。
よかったら参考にしてみて。
例として、
△ABCの面積を計算していこう。
まずは、三角形を2つくっつけて平行四辺形をつくろう!
△ABCでもおなじさ。
三角形を2つくっつけるよ。
まず△ABCをコピーして、
△A’B’C’をつくる。
んで、△A’B’C’を△ABCと合体させるんだ。
三角形が組み合わさって、
平行四辺形ABC’Dができるはず!!
これが第1ステップさ。
つぎは、平行四辺形の面積をもとめるよ。
1辺×高さ
だったよね??
平行四辺形ABC’Dの1辺の長さは6 cm、
高さは4 cm。
だから面積は、
6×4
= 24[cm^2]
になるね。
最後に、平行四辺形を三角形にもどそう。
平行四辺形の面積を2で割ってやればいいんだ。
だって、三角形が2つ含まれているからね。
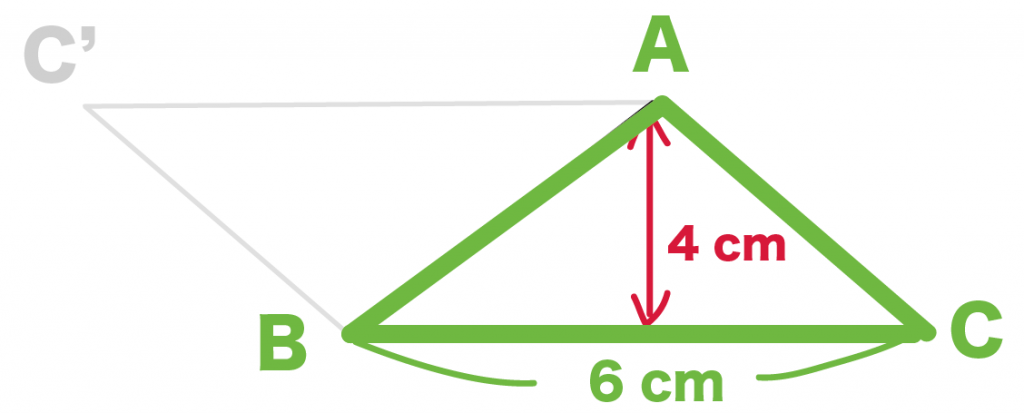
平行四辺形ABC’Dの面積は「24cm^2」だったよね??
こいつを2で割ってやると、
24 ÷2
= 12[cm^2]
になる。
おめでとう!これで三角形の面積を計算できたね!
三角形の面積の求め方はどうだった??
の3ステップでいいんだ。あとは、
底辺×高さ÷2
の公式でじゃんじゃん計算していこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。リフティング、はじめたよ。
平行四辺形の角度を求める公式ってしってる??
角度をa、その隣の角度をbとすると、
b = 180 -a
になるんだ!
たとえば、角A = 120°の平行四辺形ABCDがあったとしよう。
このとき公式をつかうと、
角B = 180 -120
= 60°
になるんだ!
どう?? むちゃ便利な公式でしょ!??
今日はせっかくだから、
なぜ公式で平行四辺形の角度が求められるのか???
ってことを振り返ってみよう。
さっきの「平行四辺形ABCD」をつかうよ。
公式なしで、角Bを計算していこう!
まずは向かいあった角を計算してやろう。
平行四辺形ABCDでいうと、角Aの角度がわかってるね??
ってことは、
向かいあっているのは「角C」だ。
「2組の向かいあう角の大きさはそれぞれ等しい」
という平行四辺形の性質をつかってあげよう。
すると、
角C = 角A = 120°
になるはずだ!
これが第一ステップ!
平行四辺形の2つの角度がわかったね。
つぎは、
残り2つの角度をたしたらいくつになる??
ってことを計算するよ。
四角形の内角の和は、
360°
だったよね??
この「360°」から2つの角度をひけばいいんだ。
平行四辺形ABCDでいうと、
「角A」と 「角C」が120°ってことがわかった。
つまり、こいつらを足すと、
240°になるはずだ。
これを四角形の内角の和360°からひいてやると、
360 – 240
= 120°
になるね。
つまり、
残りの「角BとC」をたしたら120°になる
ってわけさ。
最後は「残りの角の和」を2でわろう。
なぜ2でわるのかというと、
残り2つの角度も等しいからだよ。
だって、平行四辺形の性質の、
「向かいあう角が等しい」
ってやつが使えるからね。
平行四辺形ABCDでいうと、BとDが等しいってことなんだ。
角Bと角Dをたしたら120°になる。
しかも、角B =角Dだから、
角B + 角D = 120
角B + 角B = 120
角B = 角D = 60°
になるね。
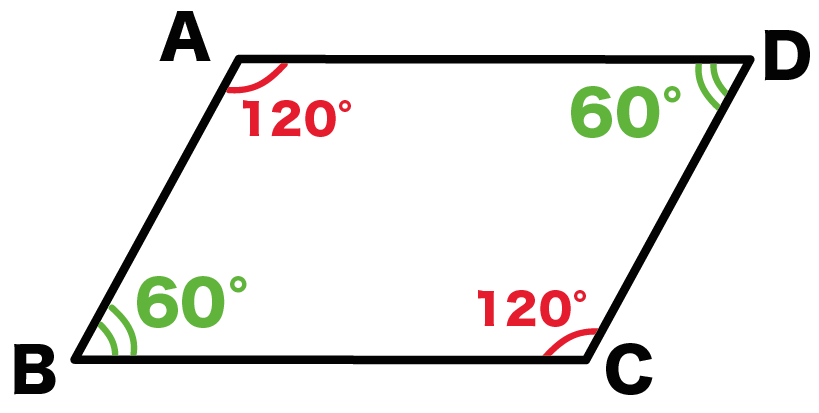
おめでとう!
平行四辺形の角度を求められたね!
平行四辺形の角度の求め方はシンプル。
180°から「隣の角の大きさ」をひけばいいんだ。
便利な公式だけど、
なぜ公式がつかえるのか??
ってことをおさえておこう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。みりんを大人買いしたね。
平行四辺形の高さの問題
ってたまーにでてくる。
たまにね。
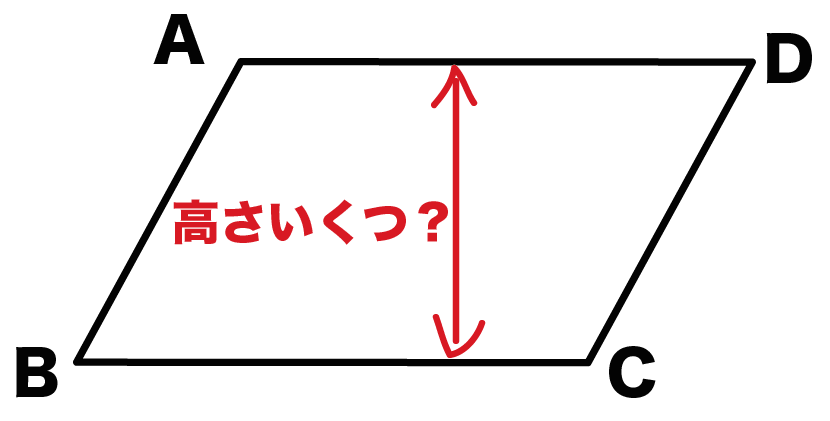
「たまーに」なら勉強しなくていいや・・・
と思うかもしれない。
けど、それは大きな間違いだ。
たまーにでるからこそ、
ライバルたちと差がつけやすい問題でもあるんだ!
今日はそんなアツいテンションで、
平行四辺形の高さの求め方
を2つ紹介するよ。
高さを求める問題には2パターンある。
平行四辺形の「面積」と「1辺の長さ」がわかっている問題だ。
ここでは、平行四辺形の面積の公式を応用してやろう。
面積をa、1辺の長さをbとすると、
高さ = a/b
で求めることができるんだ。
つまり、
(平行四辺形の高さ)=(面積)÷(1辺の長さ)
ってことだね。
たとえば、面積が36 [cm^2]、BCの長さが9 [cm]の平行四辺形があったとする。
このとき、平行四辺形の高さは、
(高さ)=(面積)÷(1辺の長さ)
= 4 [cm]
になるんだ。
このタイプの問題は公式をつかっていこう!
2つ目は、
「平行四辺形の内角」と「1辺の長さ」がわかってるパターンだ。
この問題では、
直角三角形の比をつかっていくよ。
たとえば、
平行四辺形ABCDのAB = 6 cm、角A = 120°だとしよう。
まず、
角度がわかっている頂点から垂線をおろす。
向かい側の辺にね。
平行四辺形ABCDでいうと、
AからBCに垂線をおろすよ。
交点をHとしよう。
平行四辺形の2組の向かいあう角はそれぞれ等しいから、
になるね。
んで、
△ABHに注目してみると、
角60°をふくむ直角三角形になっていることがわかるよね??
ってことは、
AB : BH : AH = 2 : 1 : √3
になっているはず。
よって、
AH = AB × √3 /2
= 6 × √3/2
= 3√3 [cm]
になるね。
こんな感じで、
垂線をひいて、直角三角形をつくっていこう!!
平行四辺形の高さの求め方はシンプル。
の2パターンおぼえておけば、問題ない。
うん、
ガンガン問題をといていこう!
まずは高さがわからない平行四辺形の面積にチャレンジしよう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。みかん、最高。
平行四辺形の面積の求め方には「公式」がある。
1辺の長さをa、高さをhとすると、面積は、
ah
で計算できちゃうんだ。
つまり、
(平行四辺形の面積)= (平行四辺形の1辺)×(高さ)
ってわけ。
たとえば、1辺が10cm、高さが6cmの平行四辺形ABCDをイメージして。
こいつの面積は、
(平行四辺形の1辺)×(高さ)
= 10×6
= 60 [cm^2]
になるんだ。
どう??
むちゃ便利な公式でしょー?!
でもでも、でもだよ?
なんでこの公式が使えるんだろう???
どうして平行四辺形の面積が「1辺×高さ」になるのか??
ちょっと気になる。。
そこで今日は、
平行四辺形の面積の求め方の公式
を3ステップで解説していくよ。
よかったら参考にしてみて。
平行四辺形の頂点から垂線を2本ひこう。
向かいの辺に垂線をひけばいいんだ。
平行四辺形ABCDでは、
の2本をひいてみたよ。
それぞれの交点をE、Fとしよう。
はしっこの三角形を移動させよう。
三角形をナイフできりとって、
移動させるイメージね。
平行四辺形ABCDでいうと、
△CDFを、
逆の辺AB側に移動させるよ。
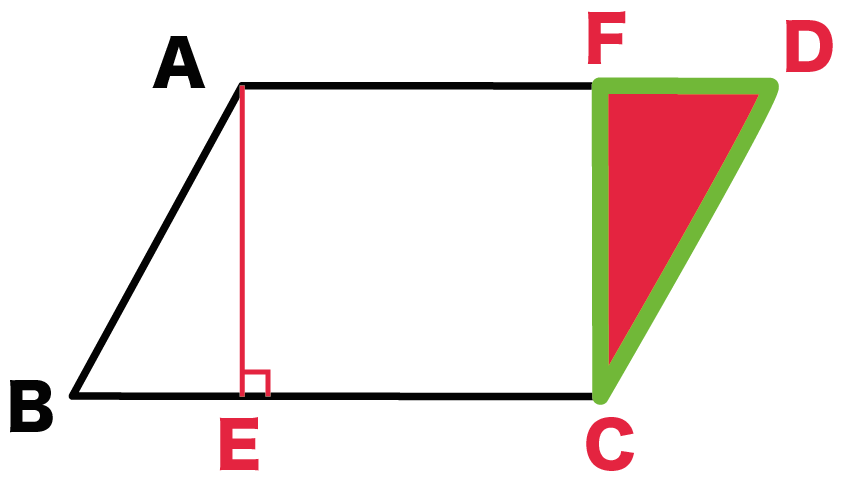
△CDFをナイフできりとって、
こいつを逆側の辺AB側に移動させてやる。
すると、
△ABEと△DCFは合同だから、
2つを組み合わせると、ぴたりとはまる。
んで、
新しいミニ長方形ができちゃうんだ。
最後は、おーきな長方形の面積を計算すればいいんだ。
ミニ三角形を移動させてできた点をGとすると、
長方形GBCFの面積でいいんだ。
長方形の面積の求め方は、
タテ×ヨコ
だったよね??
ってことは、この長方形GBCFの面積は、
GB×BC
になるわけ。
BCは平行四辺形ABCDの「1辺の長さ」、
GBは「高さ」だね。
ってことは、
長方形GBCF
= 平行四辺形ABCD
= (1辺の長さ)×(高さ)
になるんだ。
おめでとう!
平行四辺形の面積の公式をゲットしたね!
平行四辺形の面積の求め方??
そんなの簡単さ。
三角形をナイフできりとろう。
あとは、そいつを逆サイドに移動させるだけ。
1辺×高さ
の公式をじゃんじゃん使っていこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。パイナップルに埋もれたい。
平行四辺形の性質には次の3つがあったよね。
こいつらはむちゃ便利だ。
だって、
「平行四辺形」だったら、
向かいあう辺・角が等しいっていえちゃうんだからね。
しかも、対角線が中点でまじわるんだって。
こいつらを使えば、
平行四辺形の問題なんて瞬殺さ!
もー、最高だね・・・・・・
だがしかし。
なんで「平行四辺形の性質」って使えるんだろう??
便利すぎて怪しい。
詐欺かって思うよね??
そこで今日は、
平行四辺形の性質の証明を解説して、
疑問を解消していこう!
平行四辺形の性質を証明するには、
三角形の合同をつかうよ。
しかも、3組の合同を証明しなくちゃいけないんだ。
平行四辺形ABCDがあって、
対角線の交点をMとしよう。
このとき、△ABCと△ADCと、
△ABDと△CDB、
△ABMとCDMの合同を、
を証明していくんだ。
こいつらの合同がいえれば、
平行四辺形の性質を証明できるってわけ。
順番にみていくよー
まずは、平行四辺形の性質の、
2組の向かいあう辺の長さは等しい
を証明していこう。
の三角形の合同を証明していくよ!
△ABCと△CDAにおいて、
四角形ABCDは平行四辺形だから、
AD // BC・・・・(1)
だね。
平行線の性質より錯角が等しいから、
角ACB = 角CAD・・・・(2)
になる。
同じように、
AB // CDより、
錯角が等しいから、
角BAC = 角DCA・・・・(3)
んで、
辺ACは共通だから、
AC = CA ・・・・・(4)
になるね。
(2)、(3)、(4)より、
1組の辺とその両端の角がそれぞれ等しいから、
△ABC ≡ △CDA
になるね。
また、
対応する辺の長さが等しいから、
になる。
これで、平行四辺形の性質の、
「2組の辺の長さがそれぞれ等しい」
ってやつが証明できた。
つぎは2つめの、
2組の向かいあう角の大きさがそれぞれ等しい
の証明だ。
さっき証明した、
△ABC ≡ △CDA
をつかおう。
対応する角がそれぞれ等しいから、
角ABC = 角CDA・・・・(5)
ってことがいえる。
△ABC と△CDAおなじように、
△ADCと△CBAの合同
も証明できる。※ここでは省略するね。
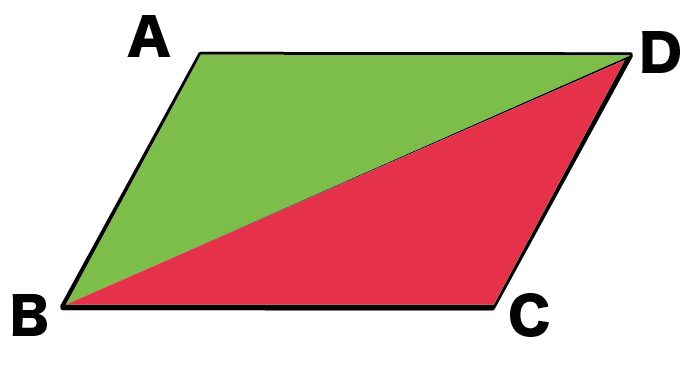
こいつらでも対応する角が等しいから、
角BAD = 角BCD・・・・(6)
ってことがいえるんだ。
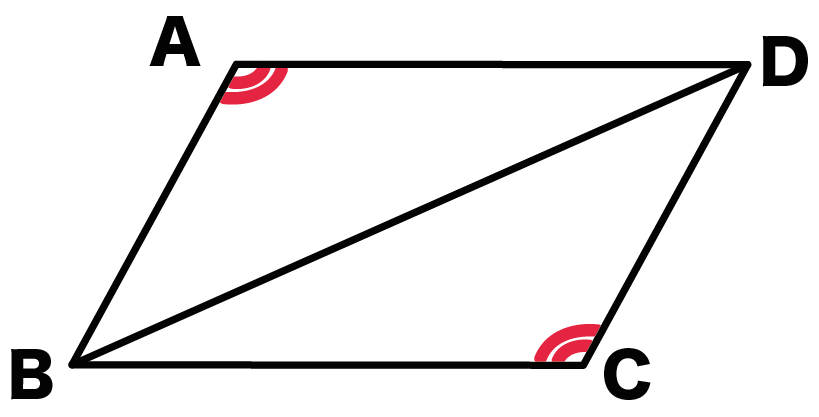
(5)・(6)より、
がいえる。
よって、
2組の向かいあう角の大きさがそれぞれ等しい
っていう性質を証明できるんだ。
最後は、
対角線はそれぞれの中点で交わる
という性質を証明していくよ。
ここでは、
△ABMと△CMDの合同
を証明していくんだ。
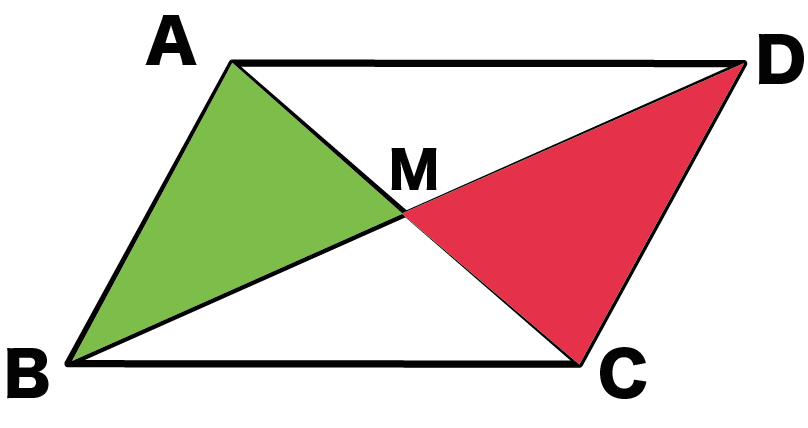
△ABMと△CMDにおいて、
さっき証明した、
「2組のむかい辺はそれぞれ等しい」
っていう性質をつかうと、
AB = CD ・・・・(1)
ってことがわかる。
AB//CDより、錯角が等しいから、
角BAM = 角DCM・・・・(2)
角ABM = 角CDM・・・・(3)
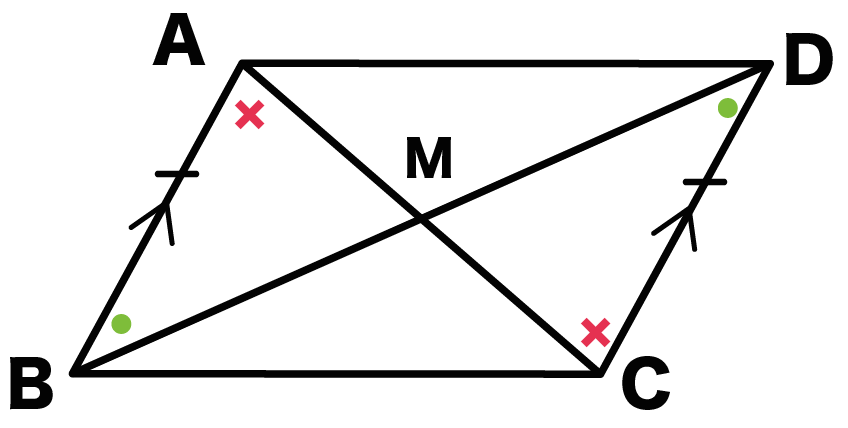
(1)、(2)、(3)より、
1組の辺とその両端の角がそれぞれ等しいから、
△ABM ≡ △CDM
になる。
よって、
対応する辺はそれぞれ等しいから、
になるよー!
つまり、
平行四辺形の対角線は中点で交わるんだ。
おめでとう!
平行四辺形の性質を3つ証明できたね。
平行四辺形の性質の証明はシンプル。
ぜーんぶ、
三角形の合同
からきているんだ。
合同な図形をしっかり見極めて、
ゆっくり証明していこう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。トースターに注意だね。
ある日、ある町で、
とある四角形に出会ったとしよう。
初めて会ったから、顔も名前も知らない。
どんな性質をもっているかわからない。
謎が多すぎるってわけ。
でも、数学を勉強している中学生ならふと、あることが気になりだす。
それは、
この四角形が平行四辺形かどうか???
だ。
こいつが平行四辺形ってことがわかれば、
親近感もわく。近づきやすくなるかもしれない。
いや、もしかしたら親友になれるかもしれない。
このように、
ある四角形が「平行四辺形かどうか」を判断するときにつかうのが、
平行四辺形になる条件
なんだ。
ぜんぶで5つあるんだけど、今日はぜんぶ紹介していくよ。
よかったら参考にしてみて。
平行四辺形の条件はぜんぶで5つある。
どれか1つをみたしていれば、
その四角形は「平行四辺形」なんだ。
えっ。
5つも多すぎておぼえられないって!??
そうだね。
でも安心して。
この5つの条件のうち、4つはみたことがあるやつでしょ??
そう。
1つめが「平行四辺形の定義」の逆で、
2~4つめが「平行四辺形の性質」の逆なんだ。
つまり、
定義と性質をおぼえていれば、条件を4つおぼえたことになる。
あとは最後の、
「1組の向かいあう辺が、等しくて平行であるとき」
だけ暗記すればいいんだ。
念のために今日は、
条件を1から振り返っていくよ。
1つめの条件は、
2組の向かいあう辺がそれぞれ平行であるとき
だ。
たとえば、ここに、
の平行四辺形ABCDがあったとしよう。
この四角形ABCDはなんと、
平行四辺形なんだ。
だって、
2組の向かいあう辺(ABとCD、ADとBC)が平行だからね。
平行四辺形の定義をみたす四角形は「平行四辺形」である
ってことをおぼえておこう。
つぎの条件は、
2組の向かいあう辺がそれぞれ等しいとき
だ。
これは平行四辺形の性質の逆をいっているね。
たとえば、四辺形ABCDの各辺が、
だったとしよう。
こいつは、
2組の向かいあっている辺が等しい
という条件をみたしている。
よって、
四角形ABCDは平行四辺形なんだ。
つぎは、
2組の向かいあう角が等しい
っていう条件だ。
これも平行四辺形の性質の逆をいっている。
たとえば、四角形ABCDのそれぞれの角が、
だったとしよう。
このとき、
向かいあう角同士が等しいから、
四角形ABCDは平行四辺形である
っていえるんだ。
4つめは、
四角形の対角線が中点でまじわっているとき
だ。
これも平行四辺形の性質の逆さ。
たとえば、
四角形ABCDの対角線を2本ひいたとき、
対角線ACとBDがMでまじわっているとしよう。
このとき、もし、
だったら、
四角形ABCDは「平行四辺形である」
っていえるんだ。
いよいよ最後の条件。
1組の向かいあう辺が等しく平行であるとき
だ。
これは平行四辺形の定義・性質の逆でもない。
オリジナルな条件なんだ。
ぶっちゃけ、
この条件さえおぼえておけば問題ない。
だって、あとは定義と性質の逆をいっているだけだからね。
たとえば、四角形ABCDで、
だったとしよう。
このとき、
1組の向かいあう辺が等しく平行である(ADとBC)
っていう条件をみたしている。
よって、
四角形ABCDは平行四辺形である
っていえるんだ!!
以上が「平行四辺形になる条件」だよ。
とくに最後の、
1組の向かいあう辺が等しく平行である
ってやつがむちゃ重要。
なぜなら、
平行四辺形の定義・性質の逆じゃないからね。
メンドイときは最後の条件だけおぼえよう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。故郷が恋しいね。
平行四辺形の定義はわかった。
だけど、
平行四辺形にはどんな性質があるんだろう??
って思うよね。
今日はそんなときに備えて、
平行四辺形の性質を3つ紹介していくよ。
よかったら参考にしてみて。
平行四辺形の性質には3つあるんだ。
うえからみていくよー!
1つ目の性質は、
2組の向かいあう辺はそれぞれ等しい
というものさ。
平行四辺形ABCDがあったしよう。
向かいあう辺どうしが等しいから、
になるんだ。
つまり、
平行四辺形の1辺がわかると、向かいあった辺の長さもわかる
ってことなんだ。
すごくない??
たとえば、
だったとしよう。
残りの辺の長さを求めてみよう。
2組の向かいあう辺の長さは等しいので、
になるんだ。
どう?
クソ便利な性質でしょ??。
つぎは角度についての性質。
2組の向かいあう角はそれぞれ等しい
というものがあるんだ。
平行四辺形ABCDがあったとしよう。
向かいあう角が等しいから、
になるんだ。
たとえば、角A = 120°だとしたら、
角C = 120°になるってこと。
しかも、
角B = 角Dってことを使えば、
残りの角の大きさもわかっちゃう。
角Bと角Dの大きさは、
(四角形の内角の和 360°)から
(角AとCをひいたもの)を(2でわったやつ)になる。
角B = 角C = (360-120-120)/2
= 60°
になるってことだ。
1つの角度がわかれば、ぜーんぶの角度がわかっちゃうんだよ。
すごいね!
いよいよ最後の性質だ。
平行四辺形の対角線は中点で交わる
ってやつだよ。
平行四辺形ABCDがあったとしたら、
対角線ACとBDは中点でまじわっているんだ。
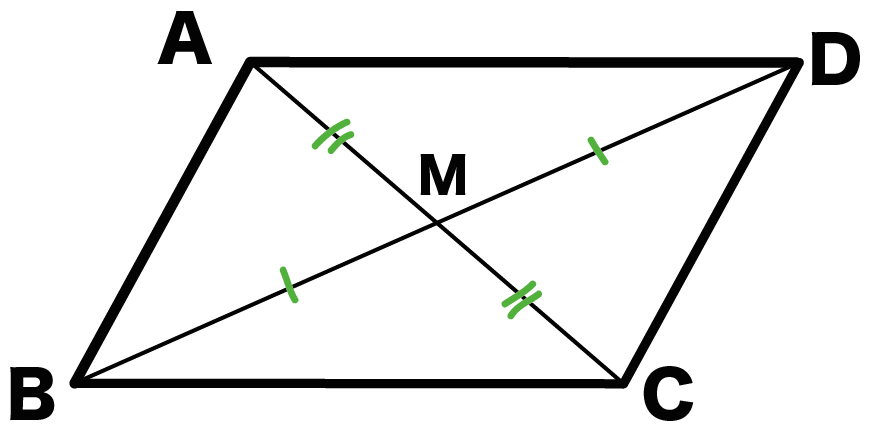
対角線の交点をMとすれば、
になってるってことさ。
たとえば、対角線ACの長さを12cmとしよう。
気分で、
もう1つ対角線BDをひいたとしよう。
交点をMとすると、
AM = CM = 6 cm
になっちゃうんだ。
つまり、
対角線ACの中点で、
ACとBDがまじわっているわけだね。
これで平行四辺形の3つの性質はおわり!
ゆっくりでいいからおぼえていこう。
平行四辺形の3つの性質はどうだった??
こいつらは意外と問題にでてくる。
テスト前にしっかりとおさえておこう!
そんじゃねー
Ken