【中学数学】平行四辺形の高さの2つの求め方
平行四辺形の高さの求め方を知りたい!
こんにちは!この記事をかいているKenだよ。みりんを大人買いしたね。
平行四辺形の高さの問題
ってたまーにでてくる。
たまにね。
「たまーに」なら勉強しなくていいや・・・
と思うかもしれない。
けど、それは大きな間違いだ。
たまーにでるからこそ、
ライバルたちと差がつけやすい問題でもあるんだ!
今日はそんなアツいテンションで、
平行四辺形の高さの求め方
を2つ紹介するよ。
平行四辺形の高さの2つの求め方
高さを求める問題には2パターンある。
- 「面積」と「1辺の長さ」がわかるヤツ
- 「内角」と「1辺の長さ」がわかるヤツ
求め方1. 「面積と1辺の長さがわかるとき」
平行四辺形の「面積」と「1辺の長さ」がわかっている問題だ。
ここでは、平行四辺形の面積の公式を応用してやろう。
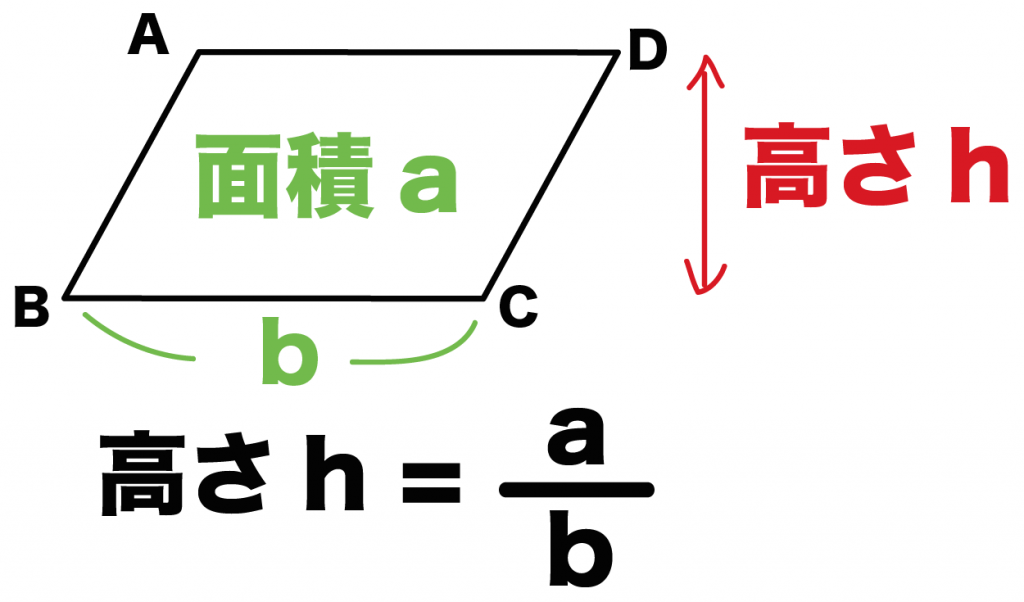
面積をa、1辺の長さをbとすると、
高さ = a/b
で求めることができるんだ。
つまり、
(平行四辺形の高さ)=(面積)÷(1辺の長さ)
ってことだね。
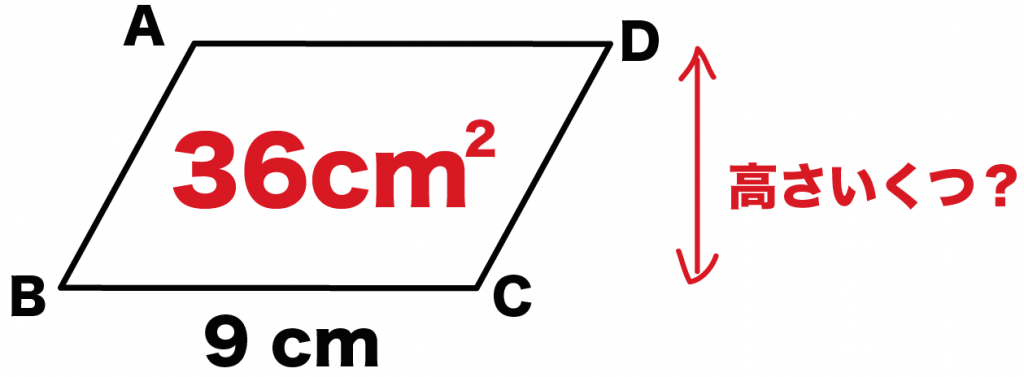
たとえば、面積が36 [cm^2]、BCの長さが9 [cm]の平行四辺形があったとする。
このとき、平行四辺形の高さは、
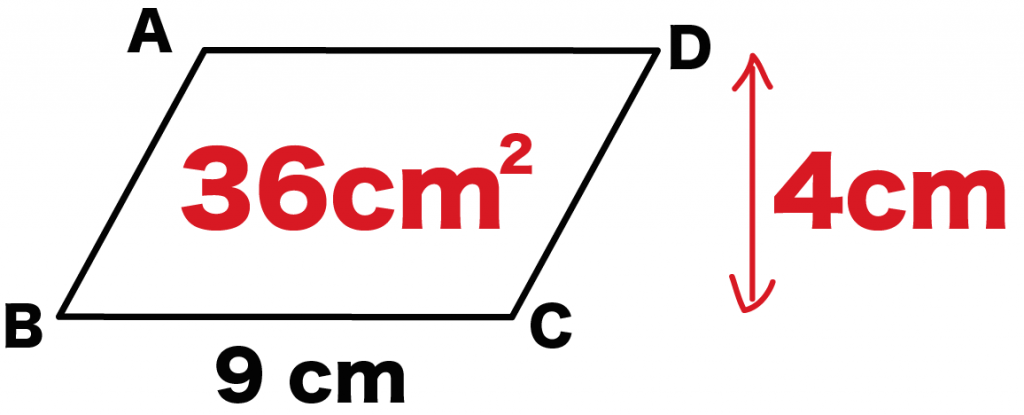
(高さ)=(面積)÷(1辺の長さ)
= 4 [cm]
になるんだ。
このタイプの問題は公式をつかっていこう!
求め方2. 「内角と1辺がわかっているとき」
2つ目は、
「平行四辺形の内角」と「1辺の長さ」がわかってるパターンだ。
この問題では、
直角三角形の比をつかっていくよ。
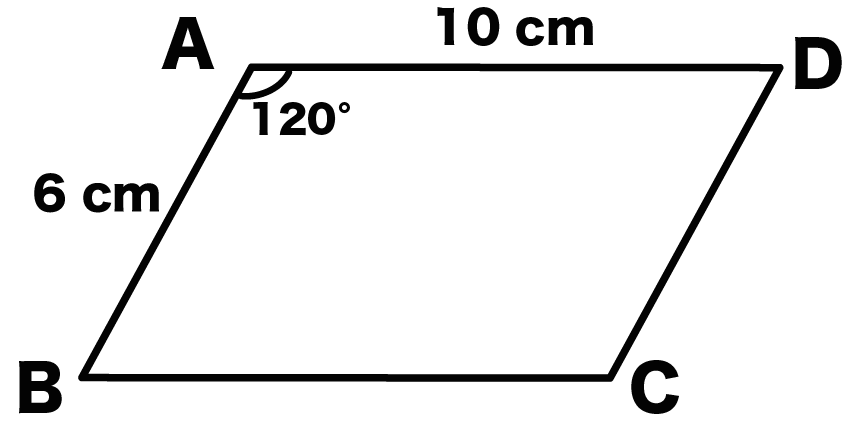
たとえば、
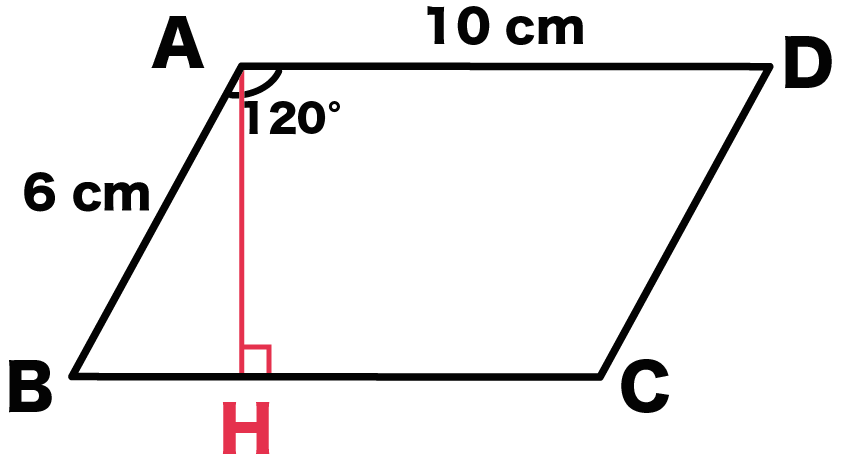
平行四辺形ABCDのAB = 6 cm、角A = 120°だとしよう。
まず、
角度がわかっている頂点から垂線をおろす。
向かい側の辺にね。
平行四辺形ABCDでいうと、
AからBCに垂線をおろすよ。
交点をHとしよう。
平行四辺形の2組の向かいあう角はそれぞれ等しいから、
- 角A = 角C = 120°
- 角B = 角D = 60°
になるね。
んで、
△ABHに注目してみると、
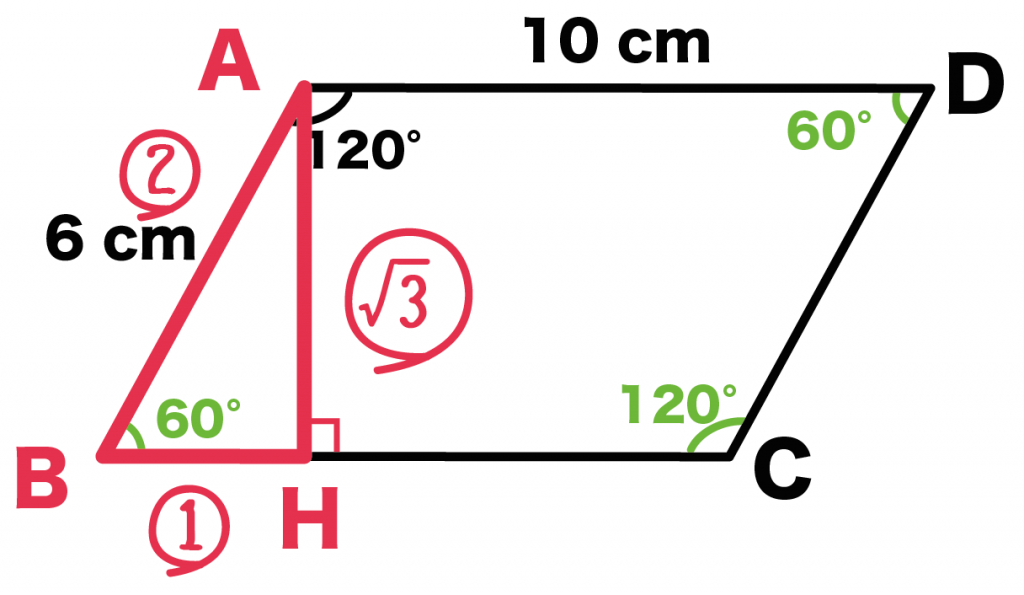
角60°をふくむ直角三角形になっていることがわかるよね??
ってことは、
AB : BH : AH = 2 : 1 : √3
になっているはず。
よって、
AH = AB × √3 /2
= 6 × √3/2
= 3√3 [cm]
になるね。
こんな感じで、
垂線をひいて、直角三角形をつくっていこう!!
まとめ:平行四辺形の高さの求め方は2つおぼえとく!
平行四辺形の高さの求め方はシンプル。
- 「面積」と「1辺の長さ」がわかるとき
- 「内角」と「1辺の長さ」がわかるとき
の2パターンおぼえておけば、問題ない。
うん、
ガンガン問題をといていこう!
まずは高さがわからない平行四辺形の面積にチャレンジしよう。
そんじゃねー
Ken