ブーメラン型四角形(凹四角形)の角度を求める方法
ブーメランみたいな図形でてきた
中学数学ではたくさん「角度の問題」が出てくるよね?
中でもなぜかでてきやすいのが、この不思議な図解↓
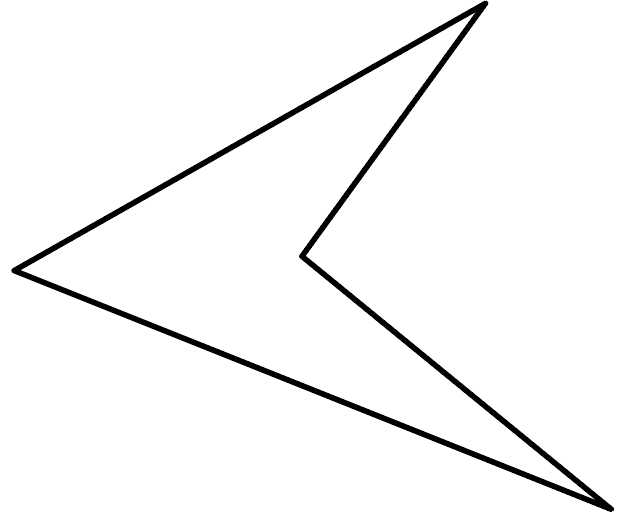
ブーメランのように見えてくるし、矢じりのようにも見えてくるし、「く」にも見えてくる。
いや、紙飛行機のようにも見えなくは、ない。
角度によっては「人」に見えるときも、ある。
じつはこの四角形にはちゃんと名前がついていて、業界では
凹四角形(おうしかくけい)
と呼んでいるんだ。
これは、
1つの内角の大きさが180度を超える四角形のこと
だね。
この問題は難しそうに見えるけど、じつはめちゃくちゃ簡単だよ。
ブーメラン型四角形の角度の求め方
この四角形が出てきたら、次の法則を覚えておけば大丈夫。
ズバリ、
「3つの尖った内角」をたすと「溝の角度」になる
っていう裏技。
たとえば、「尖った部分の角度」がそれぞれ
- a度
- b度
- c度
だとしよう。
このとき、矢じりの裂け目、ブーメランが曲っている角度は、a・b・cをぜーんぶ足した角度になるんだ。
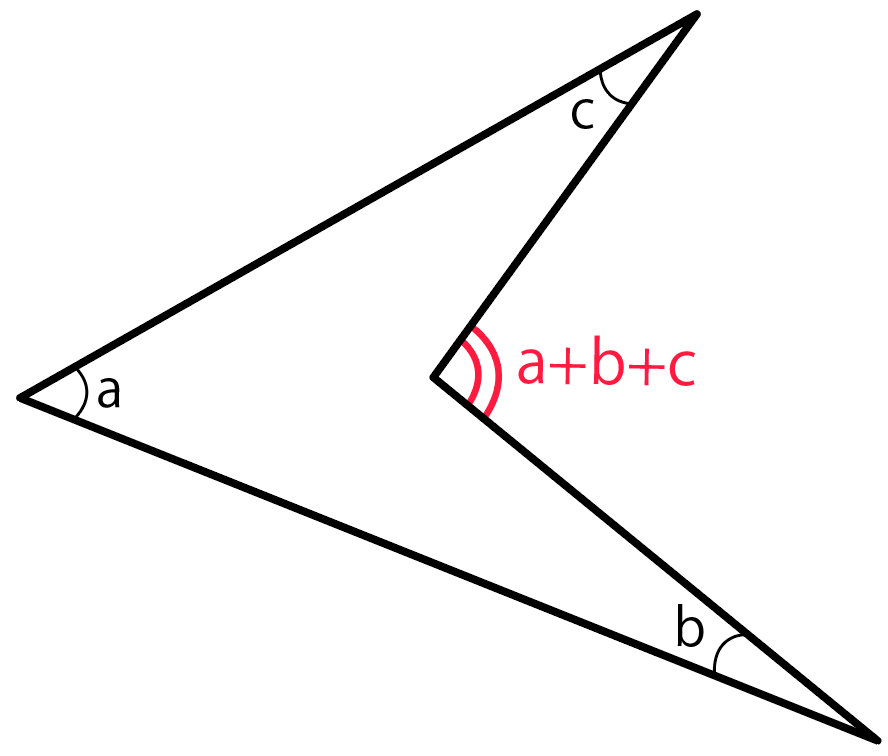
いやあ、こりゃ不思議だね。
これを応用してやると、次のような問題も一発でとけるようになるよ。
xの角度を求めなさい。
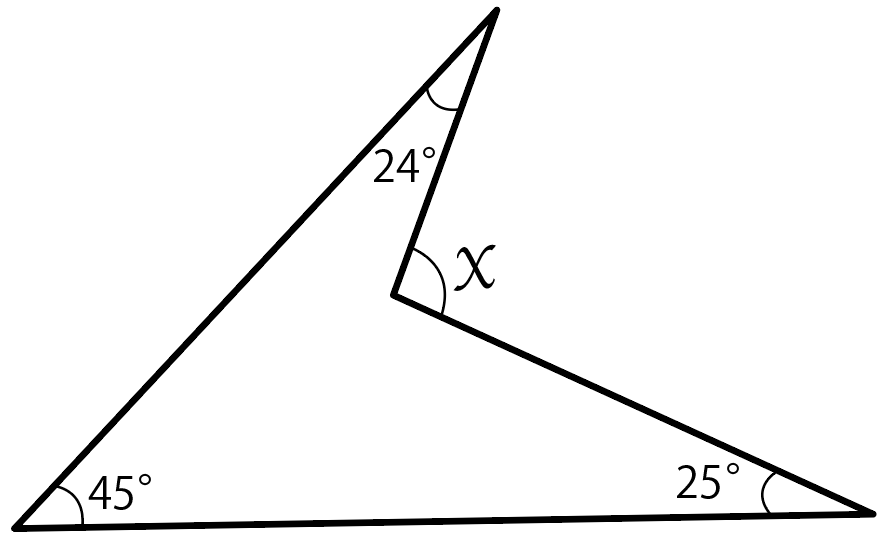
この場合、ぜーんぶの角度を足してやって、
45 + 24 + 25
= 94度
で、Xの角度は94度ってわけさ。
いやあ、ぜーんぶ足すだけなんて超楽。
なぜブーメラン型の四角形の角度は求めやすいの??
それじゃあ、なぜブーメラン型の四角形の角度は求めやすいんだろうね??
いろいろ求め方があるけど、一番しっくりきているのは三角形の外角の定理を使う方法かな。
念のために復習すると「三角形の外角の定理」とは、
2つの内角をたすと、残りの内角に接する外角になる
ってやつだったね。
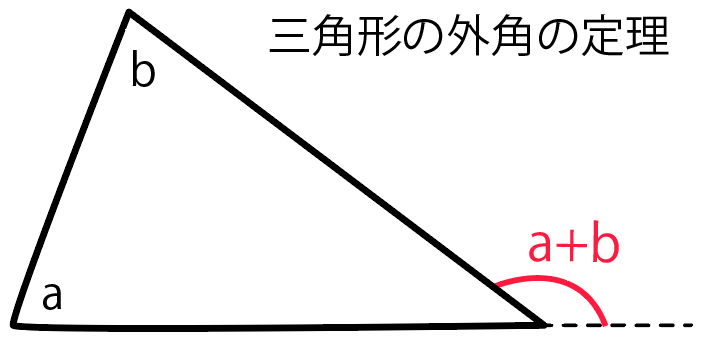
補助線を引く
まずは補助線を引いてみよう。
ブーメランの1辺から向かい側に向かって補助線を引っ張ってやる。
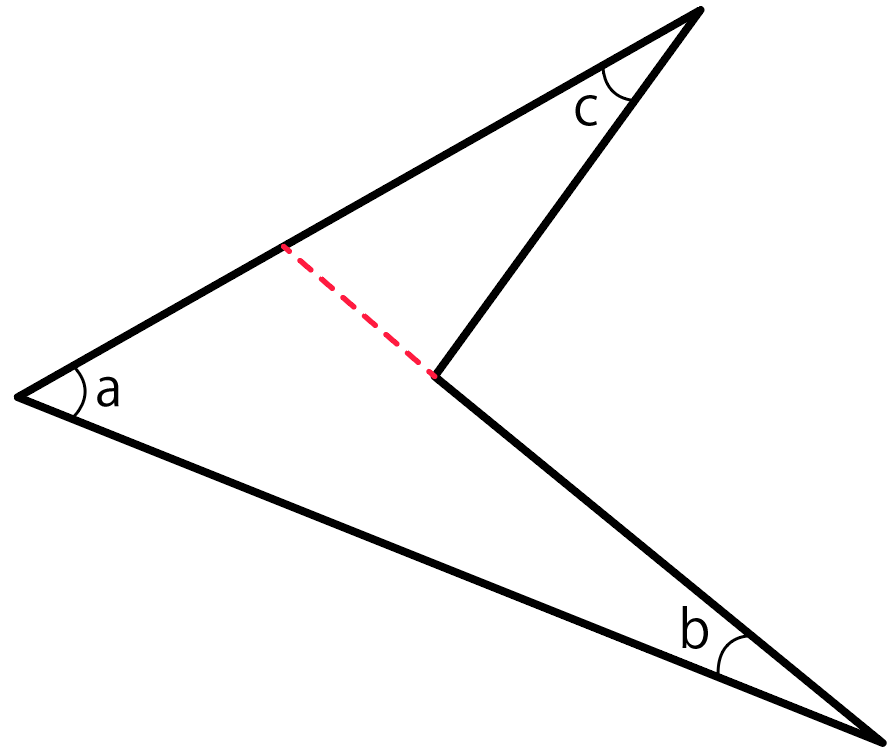
そして、三角形を2つ作る。
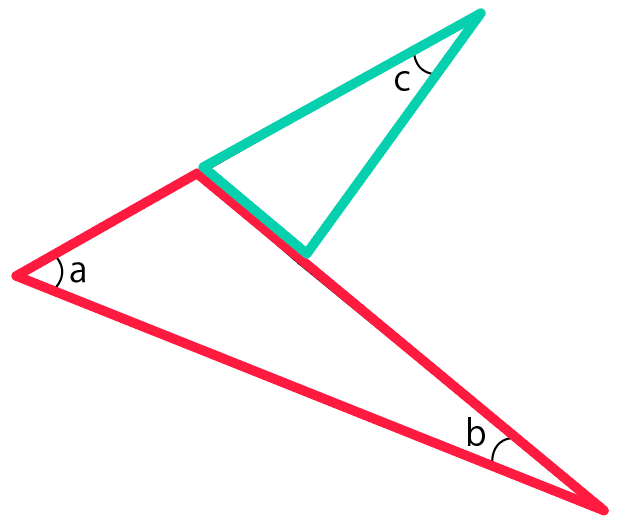
外角の定理を2回使う
あとは2つの三角形で、三角形の外角の定理を2回使うだけ。
まず手前の「赤い三角形」で外角の性質を使ってみよう。
すると、外角の大きさはaとbを足したやつになるはず。
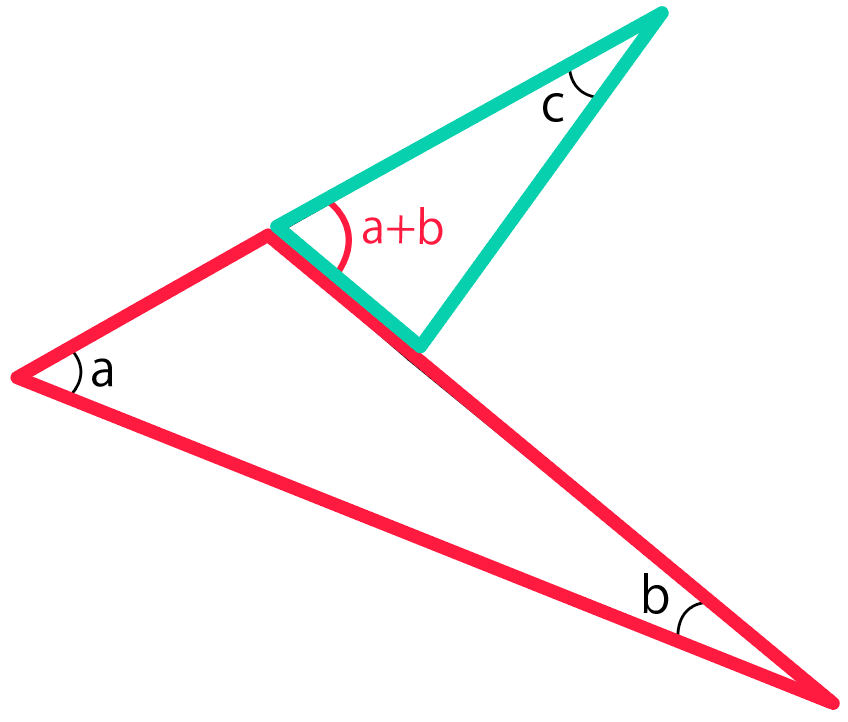
そして、緑の三角形でもう一回、外角の定理を使っていくよ。
この三角形に注目してみると、
- a+b
- c
という2つの内角になっているから、これらを足すと外角は
a+b+c
になるはずだ。
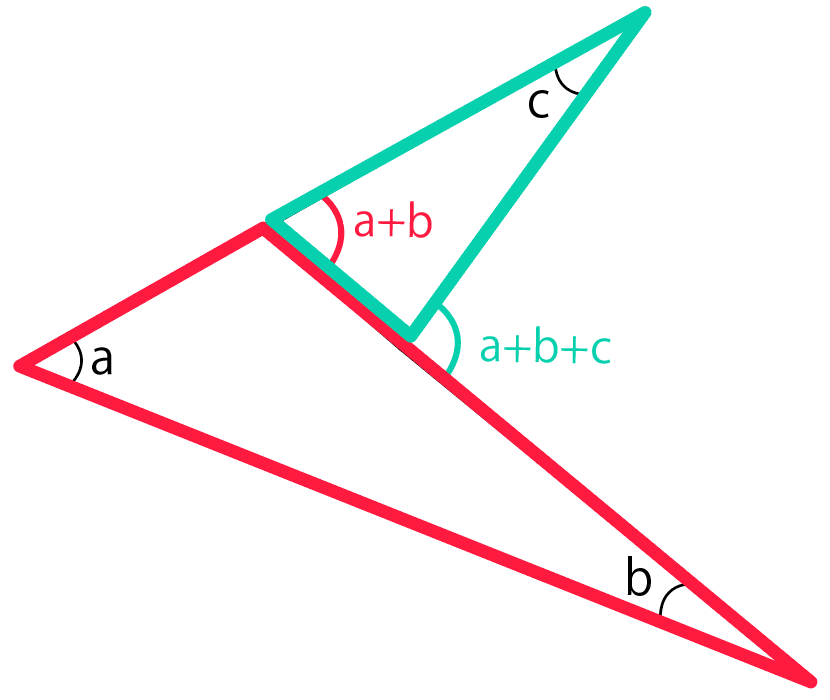
これで、ブーメランの尖ってる角度をたすと、曲っている角度になると証明できたね。
こんな感じで、ブーメラン型の四角形は解き方を知っていれば楽勝。
テストにでてきたらむしろガッツポーズしてもいい。
ただ、なぜそうなるかまで押さえておくと、応用問題まで対応できるようになるから勉強してみてね。
そんじゃねー
Ken



